
 se satisface para I y A escribiremos
«
se satisface para I y A escribiremos
« IA
IA »
. Además, habíamos hablado de una función pragmática asociada a la interpretación, la
función de evaluación que, dada una interpretación, asigna a cada variable proposicional
el valor «verdadero»
o «falso»
. Ahora en lugar de variables proposicionales hay átomos formados con predicados, y
un predicado representa a una relación de la conceptuación. Diremos que un átomo se
satisface («es verdadero»
) para una determinada interpretación y una determinada asignación si asignando los
valores a sus términos e interpretándolo, el resultado es una tupla de la relación
representada. Lo mismo que hacíamos en lógica de proposiciones, con una regla
semántica para cada una de las reglas sintácticas (Apartado 4.2) podremos establecer
las condiciones de satisfacción de cualquier sentencia:
»
. Además, habíamos hablado de una función pragmática asociada a la interpretación, la
función de evaluación que, dada una interpretación, asigna a cada variable proposicional
el valor «verdadero»
o «falso»
. Ahora en lugar de variables proposicionales hay átomos formados con predicados, y
un predicado representa a una relación de la conceptuación. Diremos que un átomo se
satisface («es verdadero»
) para una determinada interpretación y una determinada asignación si asignando los
valores a sus términos e interpretándolo, el resultado es una tupla de la relación
representada. Lo mismo que hacíamos en lógica de proposiciones, con una regla
semántica para cada una de las reglas sintácticas (Apartado 4.2) podremos establecer
las condiciones de satisfacción de cualquier sentencia:
 IAp(t1,t2,...,tn) sii (A(t1),A(t2),...,A(tn))
IAp(t1,t2,...,tn) sii (A(t1),A(t2),...,A(tn)) 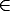 I(p)
I(p)
(Un átomo se satisface si y sólo si las asignaciones de sus términos resultan en una tupla incluida en la interpretación del predicado).
 IA(¬
IA(¬ ) sii no es el caso que
) sii no es el caso que  IA
IA
 IA(
IA(

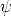 ) sii
) sii  IA
IA y
y  IA
IA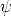
 IA(
IA(

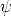 ) sii o bien
) sii o bien  IA
IA o bien
o bien  IA
IA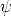 o ambos
o ambos
 IA(
IA(
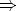
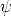 ) sii no es el caso que (
) sii no es el caso que ( IA
IA y no
y no  IA
IA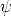 )
)
 IA(
IA(

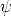 ) sii
) sii  IA(
IA(
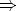
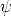 ) y
) y  IA(
IA(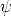
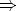
 )
)
 IA(
IA( x)(
x)( ) sii para todo c
) sii para todo c 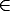 U,
U,  IA'
IA' ,
,
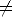 x
x
(Una sentencia cuantificada universalmente en una variable se satisface si y sólo si la sentencia que está dentro del alcance del cuantificador se satisface para todas las asignaciones de la variable cuantificada).
 IA(
IA(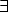 x)(
x)( ) sii para algún c
) sii para algún c 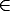 U,
U,  IA'
IA' ,
,
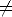 x
x
(Una sentencia cuantificada existencialmente se satisface si y sólo si la sentencia que está dentro del alcance del cuantificador se satisface para una o más de las asignaciones de la variable cuantificada).
El concepto de satisfacción define la noción relativa de verdad o falsedad en lógica de predicados: en general, una misma sentencia puede ser verdadera o falsa, dependiendo de la interpretación y de la asignación de variables (IA). Las dos últimas reglas establecen las condiciones de satisfacción para sentencias que contienen una variable cuantificada: para que la sentencia se satisfaga para una IA debe hacerlo para la asignación A de todas las variables no cuantificadas y para todas las asignaciones posibles de la variable cuantificada (en el caso de cuantificación universal) o para alguna de ellas (en el caso de cuantificación existencial).
Recordemos (Apartado 3.3.2) que una sentencia condicional sólo deja de satisfacerse en el caso de que su antecedente sea verdadero y su consecuente falso. Por ejemplo, en nuestra conceptuación de los jefes y los superiores, y con la interpretación definida por I, la sentencia
( x)(
x)( y)(jefe(x,y)
y)(jefe(x,y) 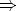 superior(x,y))
superior(x,y))
se satisface para A(x)=Agustín, A(y)=Ana, puesto que (Agustín,Ana)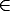 Jefe y,
asimismo, (Agustín,Ana)
Jefe y,
asimismo, (Agustín,Ana)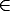 Superior, y por tanto se satisfacen el antecedente y el
consecuente. Pero también se satisface para A(x)=Mortadelo, A(y)=Filemón, puesto
que (Mortadelo,Filemón) no está ni en la relación «Jefe»
ni en la relación «Superior»
, y asimismo se satisface para A(x)=Agustín, A(y)=Andrés, ya que esta asignación no
satisface a «jefe(x,y)»
, aunque sí a «superior(x,y)»
. De hecho, con la interpretación dada, la sentencia se satisface siempre, puesto que
todas las parejas de la relación «Jefe»
están también en la relación «Superior»
. Como veremos enseguida, en este caso se dice que esa interpretación es un
«modelo»
de la sentencia.
Superior, y por tanto se satisfacen el antecedente y el
consecuente. Pero también se satisface para A(x)=Mortadelo, A(y)=Filemón, puesto
que (Mortadelo,Filemón) no está ni en la relación «Jefe»
ni en la relación «Superior»
, y asimismo se satisface para A(x)=Agustín, A(y)=Andrés, ya que esta asignación no
satisface a «jefe(x,y)»
, aunque sí a «superior(x,y)»
. De hecho, con la interpretación dada, la sentencia se satisface siempre, puesto que
todas las parejas de la relación «Jefe»
están también en la relación «Superior»
. Como veremos enseguida, en este caso se dice que esa interpretación es un
«modelo»
de la sentencia.
Y recordemos también que no debe confundirse una sentencia condicional con una «implicación» : esta última corresponde, como también veremos, a un condicional que se satisface siempre (para toda I y toda A).