es satisfactible si y sólo si existen una I y una A tales que 
IA;
en caso contrario es insatisfactible. Un conjunto de sentencias {,
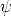,...} es
satisfactible si y sólo si existe una I y una A tales que 
IA( 
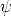
...); en caso
contrario se dice que las sentencias son inconsistentes. El ejemplo más sencillo de
sentencias inconsistentes es {p(x),¬p(x)}.
Una sentencia es válida si y sólo si, para toda I y toda A, 
IA. En este caso se
escribe «
»
. El ejemplo más sencillo de sentencia válida es p(x) 
¬p(x) («principio del tercio
excluso»
). Una sentencia válida que no contiene variables se llama tautología (Apartado 3.3.3).
Por ejemplo, p(C) ¬p(C).
Un sistema axiomático de FOL (cosa que no vamos a estudiar) es consistente si toda
ley (axioma lógico o teorema, Apartado 3.2.2), 
, es una sentencia válida, 
, y
es completo si toda sentencia válida es un axioma o un teorema que puede
demostrarse.
Dada una conceptuación, las sentencias que escribimos para representar conocimientos no son sentencias válidas (una sentencia válida, al satisfacerse siempre, no representa nada; desde el punto de vista de la teoría de la información, no proporciona información alguna). Son los axiomas del dominio (Apartado 4.1), que se supone que se satisfacen para una determinada interpretación (la interpretación pretendida), pero no para otras.
DIT-ETSIT-UPM