4.3.1.
Interpretación y asignación
Una interpretación, I, es una función que aplica elementos del lenguaje en
elementos de la conceptuación, y que debe satisfacer las siguientes condiciones:
- Si C es un símbolo de constante, entonces I(C)
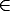 U (es decir, las
constantes representan individuos del universo del discurso).
U (es decir, las
constantes representan individuos del universo del discurso).
- Si p es un símbolo de predicado de grado n, entonces I(p)
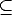 Un (es decir,
los símbolos de predicado representan relaciones de la conceptuación).
Un (es decir,
los símbolos de predicado representan relaciones de la conceptuación).
- Si f es un símbolo de función de grado n, entonces I(f) = Un
 U (es
decir, los símbolos de función representan funciones de la conceptuación).
U (es
decir, los símbolos de función representan funciones de la conceptuación).
El formalismo matemático puede ofuscar al lector, cuando en realidad el concepto
de interpretación es simple. Se trata simplemente de formalizar la noción de que los
símbolos representan las abstracciones de la realidad modelada en la conceptuación.
Como ejemplo, volvamos al «mundo de los bloques»
. En el Apartado 4.2.1 habíamos elegido ciertos símbolos, A, B... para representar a la
conceptuación, es decir, habíamos definido una interpretación. Para la situación
reflejada en la Figura 1.6, el resultado de esta interpretación es:
- I(A) = a, I(B) = b, I(C) = c, I(D) = d, I(E) = e
- I(encima-de) = Encima-de = {(b,a), (c,b), (e,d)}
- I(libre) = Libre = {a,d}
- I(base) = Base = {c,e}
- I(sobre) = Sobre = {(a,b), (b,c), (d,e)}
- I(más-arriba-que) = Más-arriba-que = {(a,b), (b,c), (a,c), (d,e)}
Bajo esta interpretación habíamos escrito estos axiomas del dominio (conocimiento
normativo, Apartado 1.3.2):
- (
 x)(
x)( y)((y = encima-de(x))
y)((y = encima-de(x))  sobre(y,x))
sobre(y,x))
- (
 x)(
x)( y)(libre(x)
y)(libre(x)  ¬(
¬(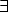 y)(sobre(y,x)))
y)(sobre(y,x)))
- (
 x)(
x)( y)(más-arriba-que(x,y)
y)(más-arriba-que(x,y)  (sobre(x,y)
(sobre(x,y)  (
(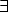 z)(sobre(x,z)
z)(sobre(x,z)  más-arriba-que(z,y))))
más-arriba-que(z,y))))
Y la situación de la Figura 1.6 (conocimiento factual) puede representarse con las
sentencias sobre(a,b), etc.
Ahora bien, esa es la interpretación pretendida, o «natural»
. Nada (salvo el sentido común) nos impide hacer esta otra interpretación del símbolo
«sobre»
:
I(sobre) = {(b,a), (c,b), (e,d)}
Este símbolo estaría ahora representando a la relación Bajo de la conceptuación. Y
bajo esta interpretación no podríamos considerar válidos los anteriores axiomas del
dominio.
Otro ejemplo, en el que el universo del discurso son personas:
U={Agustín, Ana, Andrés, Angel, Baltasar, Bartolomé, Belén, Carmen, Diego. . . }
R={Jefe, Superior}, relaciones de grado 2 definidas por:
Jefe={(Agustín, Ana), (Agustín, Baltasar), (Ana, Andrés), (Ana, Bartolomé),
(Ana, Carmen), (Baltasar, Diego), (Bartolomé, Angel), (Bartolomé, Belén)}
(Es decir, Agustín es jefe de Ana, etc.).
Superior=Jefe {(Agustín, Andrés), (Agustín, Bartolomé), (Agustín, Carmen),
{(Agustín, Andrés), (Agustín, Bartolomé), (Agustín, Carmen),
(Agustín, Angel), (Agustín, Belén), (Ana, Angel), (Ana, Belén),
(Agustín, Diego)}
(Es decir, todas las parejas que están en la relación «Jefe»
están también en la relación «Superior»
, y, además, Agustín es superior de Andrés, etc.).
Creando los símbolos A1, A2... para las constantes y jefe y superior para los
predicados, con la interpretación pretendida:
I(A1)=Agustín; I(A2)=Ana; I(A3)=Andrés; I(A4)=Angel;
I(B1)=Baltasar; I(B2)=Bartolomé; I(B3)=Belén;
I(C1)=Carmen; I(D1)=Diego
I(jefe) = Jefe
I(superior) = Superior
podemos representar el conocimiento factual con las sentencias: jefe(A1,B1),
etc, y un conocimiento normativo con una sentencia que define la relación
«Superior»
en función de «Jefe»
:
( x)(
x)( y)(superior(x,y)
y)(superior(x,y)  (jefe(x,y)
(jefe(x,y)  (
(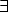 z)(jefe(x,z)
z)(jefe(x,z)  superior(z,y))))
superior(z,y))))
(definición recursiva similar a la de Más-arriba-que del mundo de los bloques).
Sin embargo, con una interpretación I' igual a I para las constantes pero tal
que:
I'(jefe)={(Ana, Agustín), (Baltasar, Agustín), (Andrés, Ana), (Bartolomé, Ana),
(Carmen, Ana), (Diego, Baltasar), (Angel, Bartolomé), (Belén, Bartolomé)}
estaríamos interpretando (supuesto que la realidad no ha cambiado, o sea, que la
relación «Jefe»
es la misma) que el símbolo «jefe»
significa en realidad «Subordinado»
(y la sentencia que define «superior»
no podría ser considerada una axioma del dominio).
En este ejemplo hemos definido la relación «Superior»
de dos maneras: extensionalmente e intensionalmente (y, como es fácil comprobar,
con la interpretación pretendida ambas coinciden). Pero lo normal será tener
algunas relaciones básicas, dadas por su extensión (que representa una situación
particular) y otras definidas intensionalmente. A partir de las primeras, un sistema
deductivo debe ser capaz de obtener las extensiones de las relaciones definidas
intensionalmente.
Asignación de términos
Una asignación de variables, A, es una función que hace corresponder elementos de U
a las variables que figuran en las sentencias. Las constantes corresponden a los
elementos de U según define la interpretación, y las funciones se aplican también en
elementos de U, según su interpretación. En general, dada una interpretación I
y una asignación de variables A, podemos extender A a una asignación de
términos:
- Si c es un símbolo de constante, A(c) = I(c);
- Si f es un símbolo de función, A(f(t1,t2,...,tn)) = F(x1,x2,...xn),
donde F = I(f) y xi = A(ti)
Por ejemplo, en el mundo de los bloques, si asignamos a la variable x el bloque b, la
asignación de la función encima-de(x) será:
A(encima-de(x)) = Encima-de(A(x)) = Encima-de(A(b)) = a
En el ejemplo de los jefes y superiores, supongamos que a la conceptuación anterior
añadimos la función de grado 1 «FJefe»
, que aplicada a Ana da como resultado Agustín, aplicada a Baltasar da como resultado
Agustín, etc. («FJefe»
contiene la misma información que la relación «Jefe»
pero expresada como función). Representemos esta función con el símbolo
«fjefe»
, es decir, I(fjefe)=FJefe y consideremos el término t = fjefe(fjefe(x)). Dada, por
ejemplo, la asignación de variables x=Andrés, resulta:
A(t) = A(fjefe(fjefe(x))) = FJefe(A(fjefe(x))) = FJefe(FJefe(A(x)) =
FJefe(FJefe(Andrés)) = Agustín
Un átomo que tiene todos sus términos asignados se llama átomo terminal (ground
atom).




 DIT-ETSIT-UPM
DIT-ETSIT-UPM
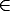 U (es decir, las
constantes representan individuos del universo del discurso).
U (es decir, las
constantes representan individuos del universo del discurso).
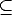 Un (es decir,
los símbolos de predicado representan relaciones de la conceptuación).
Un (es decir,
los símbolos de predicado representan relaciones de la conceptuación).
 U (es
decir, los símbolos de función representan funciones de la conceptuación).
U (es
decir, los símbolos de función representan funciones de la conceptuación).