
 y
y  son sentencias equivalentes si y sólo si
son sentencias equivalentes si y sólo si 

 y
y 

 , o, lo que es lo
mismo,
, o, lo que es lo
mismo,  (
(

 ). Expresaremos que
). Expresaremos que  y
y  son equivalentes con la notación:
son equivalentes con la notación:



Equivalencias son, por ejemplo, las leyes conmutativas y asociativas de la
conjunción y la disyunción: 





 ;
; 
 (
(

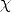 )
)  (
(

 )
) 
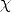





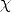 ,
etc.
,
etc.
He aquí otras equivalencias entre sentencias que utilizaremos más adelante (omitimos las demostraciones, que no son difíciles: basta tener en cuenta la definición de implicación y las reglas semánticas de satisfacción de sentencias):
 )
) 



 )
)  ¬
¬
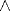 ¬
¬

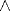
 )
)  ¬
¬
 ¬
¬

 (
(
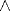
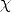 )
)  (
(

 )
) 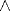 (
(

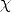 )
)

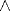 (
(

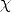 )
)  (
(
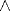
 )
)  (
(
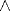
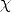 )
)


 )
) 
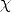
 (
(

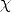 )
) 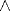 (
(

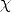 )
)

 (
(
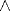
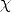 )
)  (
(

 )
) 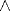 (
(

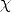 )
)

 (
(

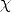 ))
))  (
(
 (
(

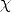 ))
))


 )
)  (¬
(¬

 )
)

 (
(
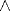 ¬
¬ ))
)) 

La equivalencia (1) es bastante obvia, y corresponde a la ley de la doble negación
de la lógica clásica. El lector debe reconocer por su forma a (2) y (3): son las leyes de
de Morgan del álgebra de Boole. De (4) a (7) son leyes distributivas de la
conjunción, la disyunción y el condicional. La (8) permite intercambiar antecedentes
de condicionales encadenados, y la (9) expresar un condicionales como una
disyunción. La (10) puede parecer algo extravagante a primera vista, pero no es
otra cosa que la expresión en forma de equivalencia de la ley de reducción al
absurdo: si de la negación de  se sigue una contradicción entonces puede
afirmarse
se sigue una contradicción entonces puede
afirmarse  (y al revés: si
(y al revés: si  se satisface entonces de su negación saldrá alguna
contradicción).
se satisface entonces de su negación saldrá alguna
contradicción).
Es sabido que una relación de equivalencia en un conjunto lo particiona en clases de
equivalencia. Aunque con la gramática generativa pueden derivarse infinitas
sentencias, el número de clases de equivalencia está limitado por el número de
variables proposicionales. En el Apartado 3.3.1 hemos visto que con dos variables
proposicionales las diferentes interpretaciones pueden clasificarse en cuatro clases, las
que corresponden a las cuatro posiblidades de evaluación de las dos variables. En este
caso (dos variables proposicionales), las infinitas sentencias se clasifican por la
relación de equivalencia en 24 = 16 clases: la clase C
0 comprende todas aquellas
que no se satisfacen nunca (contradicciones, todas equivalentes a p 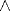 ¬p),
la clase C1 las que se sólo se satisfacen para la clase de interpretaciones I3
(equivalentes a p
¬p),
la clase C1 las que se sólo se satisfacen para la clase de interpretaciones I3
(equivalentes a p 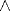 q)... la clase C15 las que se satisfacen en todas las interpretaciones
(tautologías).
q)... la clase C15 las que se satisfacen en todas las interpretaciones
(tautologías).
En general, con n variables proposicionales hay 2n clases de interpretaciones y 2(2n) clases de equivalencia entre sentencias.