¬p. Dos o más
sentencias son inconsistentes si su conjunción es insafisfactible. Por ejemplo,
{p,¬p}.
Una tautología es justamente lo opuesto: una sentencia que se satisface sea cual sea
la interpretación de sus variables proposicionales. Para indicar que una sentencia es
una tautología se utiliza el mismo símbolo de satisfacción sin el subíndice:
«
»
.
Un ejemplo es la sentencia del Apartado anterior: 
(p 
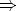(q 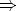p)). Y otro, la
conocida «ley del tercio excluso»
: 
(p 
¬p).
En el Apartado 3.2.2 decíamos que una ley (axioma o teorema) del cálculo es una
sentencia siempre verdadera: 
significa « es una ley»
. Pero, aunque deben coincidir, no es lo mismo, en rigor, « »
que «
»
: un teorema se demuestra dentro del cálculo, mediante transformaciones sintácticas;
una tautología es un concepto semántico. Ambas cosas coinciden si el sistema
axiomático es consistente (es decir, toda ley es una tautología) y completo (es
decir, toda tautología puede demostrarse como teorema), y el sistema PM lo
es.
Como también decíamos allí, lo que nos interesa no son los sistemas axiomáticos, sino los sistemas deductivos (Apartado 3.7), en los que, como veremos, también hay que estudiar la consistencia y la compleción.
DIT-ETSIT-UPM