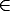4.1. Conceptuaciones

• Un universo del discurso, U, conjunto (que puede ser infinito) de individuos u objetos a considerar.
• Un conjunto finito (que puede ser vacío), R, de esquemas de relación entre los elementos de U.
• Un conjunto finito (que puede ser vacío), F, de esquemas de función que hacen corresponder a ciertos elementos de U otros elementos de U.
• Definiciones de las relaciones y funciones declaradas en los esquemas, que pueden ser:
  • extensionales, es decir, la relación (o función) se define enumerando todas las tuplas (o todas las correspondencias entre objetos) que la forman, o
  • intensionales, es decir, la relación (o función) se define a partir de otras relaciones o funciones mediante enunciados compuestos con ellas y con las partículas «y» , «o» , «no» , «si... entonces...» , «si y sólo si» , «para todos los objetos de U...» y «existe al menos un objeto en U tal que...» .

Recordemos que una definición extensional de una relación de grado n es un subconjunto del producto cartesiano Uⁿ, es decir, es un conjunto de tuplas {<e_i1,e_i2...e_in>}, donde e_ij 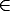U. Una propiedad es una relación de grado 1. Una definición extensional de una función de grado n es una aplicación Uⁿ U, es decir, hace corresponder a cada combinación de n elementos de U otro elemento de U.

Las definiciones extensionales expresan conocimiento sobre situaciones particulares de los objetos de U (conocimiento factual). Las definiciones intensionales expresan conocimiento normativo sobre el dominio (Apartado 1.3.2), y, una vez formalizados en el lenguaje de FOL, se llaman (como en lógica de proposiciones, Apartado 3.7.4) axiomas propios o axiomas del dominio.

Como ejemplo, podemos volver sobre el «mundo de los bloques» del Apartado 1.7, donde declarábamos:

• U = {a,b,c...} (conjunto de bloques)
• F = {Encima-de}
• R = {Libre, Base, Sobre, Más-arriba-que}

La función y las relaciones se pueden definir todas de manera extensional (como se hacía en el ejemplo original de Genesereth y Nilsson), y entonces la conceptuación es una abstracción de una situación particular (la de la Figura 1.6, o la de la Figura 1.7, etc). O, como allí hacíamos, se pueden definir intensionalmente Encima-de, Libre, Base, y Más-arriba-que en términos de Sobre, lo que expresa conocimiento normativo sobre el dominio.

Obsérvese que la noción de «verdad» o «falsedad» de un enunciado, que en lógica de proposiciones se declaraba explícitamente, o se calculaba, está implícita en la conceptuación, desde el momento en que los «enunciados» son declaraciones de relaciones. En lugar de enunciar «llueve en Madrid (valor: verdadero)» (Apartado 3.1) declararíamos la propiedad «llueve en» , definida extensionalmente como un conjunto de lugares en los que llueve. Y no diríamos «llueve en Madrid (valor: verdadero)» , sino que incluiríamos a Madrid en ese conjunto.

 DIT-ETSIT-UPM