Apéndice B :

Desarrollo de algunas expresiones matemáticas

B.1 Relación entre consistencia y k-consistencia borrosas

En este apartado demostraremos que las expresiones:

[EC. 4.29] : C es consistente sobre T ¤ ("t T) (SB(t) )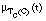

[EC. 4.30] : C es k-consistente sobre T ¤ TC(C) « P k · TC(C), para k [0, 1]

definidas en el apartado 4.3.2.6 , son equivalentes entre sí para el valor k=1. Además, la segunda es una generalización de la primera para cualquier k (es decir, toda cláusula consistente es también k-consistente).

• Demostración "toda cláusula consistente es k-consistente (la condición de k-consistencia es una generalización de la consistencia)": [EC. 4.29] [EC. 4.30] , para cualquier valor k [0, 1]

Partiendo de la [EC. 4.29] y aplicando la función

f(x) = min( , x)

a ambos lados de la desigualdad no se altera el sentido de la misma:

("t T) (min( , SB(t)) min( , ))

El parámetro k toma valores en el intervalo [0, 1], por tanto, se puede introducir como factor en la parte derecha de la desigualdad:

("t T) (min( , SB(t)) k · )

Tomando el sumatorio en las tuplas en que se cumple ("t T) se llega a:

( , SB(t) ) k · ( ) ¤

¤ TC(C) « P k · TC(C)

que es exactamente la expresión [EC. 4.30] .

 

• Demostración "toda cláusula k-consistente para k=1 cumple la condición de consistencia": [EC. 4.29] [EC. 4.30] , cuando k = 1

Partiendo de [EC. 4.30] , se puede expresar la cardinalidad escalar en forma de sumatorio, y sustituir el parámetro k = 1:

( , SB(t) ) ( )

Supongamos ahora que el conjunto T se parte en dos subconjuntos del siguiente modo:

T1 = { t T SB(t) }

T2 = { t T SB(t) < }

en ese caso, la condición anterior queda:

+ SB(t)  (

SB(t)  (

 

que sólo puede cumplirse cuando T2 es el conjunto vacío. Por tanto, todas las tuplas de T deben cumplir la expresión [EC. 4.29] :

("t T) (SB(t) )

B.2 Cálculo de NumLit(m,u)

Denominamos:

NumLit(m,u) al número de literales afirmativos distintos, construidos a partir de un predicado qm de grado m, que son candidatos a ser el siguiente antecedente de una cláusula en construcción con u variables usadas.

Todos los literales candidatos deben tener, al menos, una variable usada, por tanto, si se denomina:

NumLitJ(m,u) al número de literales afirmativos distintos con variables usadas en J términos, construidos a partir de un predicado qm de grado m, que son candidatos a ser el siguiente antecedente de una cláusula en construcción con u variables usadas.

se cumple que:

NumLit(m, u) = [EC. B.1]

En el apartado B.2.1 se calcula la expresión de NumLitJ(m,u) que, sustituida en la ecuación anterior, da lugar a la expresión:

NumLit(m, u) = [EC. B.2]

donde:

anynew(i) = número de diferentes combinaciones de variables nuevas para una tupla con i términos; este valor se calcula en el apartado B.2.2

B.3 Estimación del número medio de tuplas expandidas con las que debe evaluarse un literal

Sea un conjunto con N tuplas, todas expandidas a partir de una única tupla original. Supongamos que M de ellas satisfacen un literal Li candidato. ¿Con cuántas habrá que evaluar, en media, hasta encontrar una de estas M tuplas?

• La probabilidad de que la primera tupla elegida sea una de las M que satisfacen el literal Li será:

P1 =

• La probabilidad de que haya que evaluar dos tuplas será la probabilidad de que la primera no sea ninguna de las M y la segunda sí lo sea:

P2 =

• La probabilidad de que haya que evaluar tres tuplas será la probabilidad de que la primera no sea ninguna de las M, la segunda tampoco y la tercera sí lo sea:

P3 =

• En general, la probabilidad de que haya que evaluar n tuplas hasta encontrar una de las M que satisfacen al literal será:

Pn =

Por tanto, se puede calcular el número medio de tuplas con las que debe evaluarse Li hasta encontrar una de las M que lo satisfacen:

NumEva =

Sustituyendo los diferentes valores calculados para Pn se llega a la siguiente expresión:

NumEva = [EC. B.8]

Se puede comprobar que esta ecuación se reduce a la siguiente, sin más que desarrollar el sumatorio y simplificar términos:

NumEva = [EC. B.9]