Capítulo 4 :
En este capítulo trataremos de generalizar todos los conceptos relacionados con la lógica de predicados de primer orden, para poder aplicarlos en el caso de lógica borrosa. Como veremos, las principales diferencias se producen en la semántica asociada en uno u otro caso.
A continuación se describirá el sistema FZFOIL, construido a partir de FOIL, para inducir conocimiento con incertidumbre a partir de bases de datos relacionales borrosas.
Aunque existe gran cantidad de trabajos enfocados a formalizar la lógica borrosa, desde un punto de vista matemático, la mayoría de ellos están orientados hacia la lógica de proposiciones o la lógica de proposiciones extendida; por ejemplo, [Fernández y Sáez-Vacas, 95] constituye una buena referencia. Sin embargo, no hemos encontrado ningún trabajo en el que se trate la lógica borrosa de predicados, más allá de la simple definición de relaciones borrosas (apartado A.3 ).
¿Puede pensarse que, conocida la lógica de primer orden y la lógica borrosa de proposiciones, se conoce la lógica borrosa de predicados? Sin duda, algunas de las definiciones (como las referentes a la sintaxis o algunas referentes a la semántica como la asignación de variables) no varían al pasar de la lógica clásica de predicados a la lógica borrosa de predicados, pero otras (satisfacción, sentencias condicionales, etc.) son diferentes y, aunque son una extensión de la versión booleana, conviene definirlas de antemano, ya que podrían existir otras extensiones válidas.
La sintaxis que utilizaremos en lógica borrosa de primer orden es la misma que se utiliza en la lógica clásica de predicados de primer orden, y que puede verse, por ejemplo, en [Fernández y Sáez-Vacas, 95] . Se utilizarán las mismas definiciones para términos, fórmulas atómicas, secuencias de formación, sentencias, cuantificadores, etc.
Desde el punto de vista de la semántica es donde se producen los mayores cambios al pasar de lógica booleana a lógica borrosa. Por ello redefiniremos los principales conceptos relacionados con la semántica, generalizándolos a partir de su definición para lógica booleana (pueden verse también en [Fernández y Sáez-Vacas, 95] ).
En lógica borrosa de predicados se define una conceptualización como un modelo conceptual que consta de:
Una relación borrosa P de grado n es un subconjunto borroso del producto cartesiano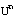 
(apartado A.3
), es decir, un subconjunto borroso de tuplas:
Una propiedad borrosa es una relación borrosa de grado 1. En el conjunto R pueden existir también relaciones ordinarias, pues éstas se consideran un caso particular de relación borrosa.
Una interpretación i, en lógica borrosa, se define del mismo modo que en lógica booleana: es una función que aplica elementos del lenguaje en elementos de la conceptualización, y que debe satisfacer las siguientes condiciones:
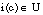(es decir, las constantes representan individuos del universo del discurso).
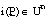(es decir, los símbolos de predicado representan relaciones borrosas de la conceptualización).Por tanto, el concepto de interpretación no es más que una formalización de la noción de que los símbolos representan aspectos de la realidad modelada en la conceptualización. Y hacer una conceptualización no es más que acotar la realidad, es decir, listar todos los individuos u objetos a considerar y todas las relaciones entre ellos.
Una asignación de variables, A, es una función que hace corresponder elementos de U a las variables que figuran en las sentencias. Las constantes corresponden a los elementos de U según define la interpretación, y las funciones se aplican también a elementos de U, según su interpretación. En general, dada una interpretación i y una asignación de variables A, podemos extender A a una asignación de términos:
El conjunto de valores de verdad en lógica borrosa lo definimos como el conjunto de números reales en el intervalo unidad: V = [0, 1].
Definimos la evaluación de una sentencia S, para una asignación de variables A y una interpretación i, y la representamos como E(S, A, i), a una función que asigna un valor del conjunto de valores de verdad a dicha sentencia.
En una conceptualización, diremos que una interpretación conjuntamente con una asignación de variables, iA, satisface en grado s a una sentencia si el valor de evaluación de la sentencia para esa iA es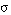 
. También diremos que la sentencia se satisface en grado 
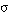para esa iA.
La notación para expresar que la sentencia S se satisface en grado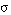 
para iA es: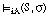 
Si para cada una de las reglas sintácticas de la lógica borrosa de predicados de primer orden establecemos las condiciones bajo las cuales la sentencia se satisface, estas condiciones definen la semántica de la lógica borrosa de primer orden. Son las siguientes:
(una fórmula atómica se satisface en grado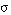 
si y sólo si las asignaciones de sus argumentos resultan en una tupla incluida con un grado de verdad 
en la interpretación del predicado).
(la negación de una sentencia se satisface en grado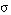 
si y sólo si la sentencia sin negar se satisface en grado 1-
).
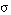(la conjunción de dos sentencias se satisface en grado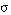 
si y sólo si el menor de los grados de satisfacción de cada una de ellas es 
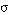; esta condición puede generalizarse a la conjunción de un número cualquiera de sentencias).
(la disyunción de dos sentencias se satisface en grado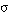 
si y sólo si el mayor de los grados de satisfacción de cada una de ellas es 
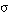; esta condición se puede generalizar a la disyunción de un número cualquiera de sentencias).
(una sentencia bicondicional se satisface en grado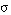 
si y sólo si el menor de los grados de satisfacción de los dos condicionales en que puede descomponerse es 
).
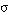(una sentencia cuantificada universalmente en una variable se satisface en grado s si y sólo si la sentencia que está dentro del alcance del cuantificador se satisface en grado s para todas las asignaciones de la variable cuantificada).
En lógica borrosa de predicados definimos un calificador borroso de verdad V como una función que modifica el grado de verdad de una sentencia borrosa S (por analogía a la definición de calificador borroso de verdad en lógica borrosa de proposiciones, apartado A.4.2.1 ).
La forma de una sentencia S' con calificador borroso de verdad es la siguiente:
El calificador borroso V se representa por una etiqueta lingüística ("verdadero", "muy verdadero", "algo verdadero", "muy falso", etc.) que se aplica sobre los valores de verdad de la sentencia borrosa S. Las funciones asociadas a estos calificadores pueden verse en el Apéndice A , figura A-1 .
El grado de satisfacción de la sentencia S', resultante de aplicar el calificador borroso de verdad V sobre una sentencia borrosa S, se calcula como el resultado de aplicar una función V, que representa al calificador, sobre el grado de satisfacción de S:
En lógica borrosa de predicados definimos un calificador borroso de probabilidad P como una función que describe una restricción en la distribución de probabilidad asociada a una sentencia S (para la lógica borrosa de proposiciones puede verse la definición correspondiente en el apartado A.4.2.2 ).
La forma de una sentencia S' con calificador borroso de probabilidad es la siguiente:
siendo Pro(S) una probabilidad asociada a la sentencia S, y P un calificador borroso de probabilidad.
Los posibles valores de P se representan con etiquetas de la forma: "probable", "muy probable", "improbable", etc. cuyo significado viene dado por curvas como las representadas en el Apéndice A , figura A-3
El grado de satisfacción para la sentencia S' con calificador borroso de probabilidad será:
Muchos sistemas de aprendizaje tradicionales son capaces de inducir conocimiento incierto: ID3 ( [Quinlan, 86] ), C4.5 ( [Quinlan, 93] ), etc., dado que asignan un factor de incertidumbre, en forma de probabilidad, al conocimiento inducido. Este tipo de representación de la incertidumbre en el conocimiento inducido también es aplicable a sistemas de aprendizaje de ILP: FOIL ( [Quinlan, 90] ), FOCL ( [Pazzani et al., 91] ), mFOIL ( [Dzeroski, 91] ), etc. En general, esta probabilidad puede calcularse a partir del conjunto de entrenamiento o de un conjunto de ejemplos de prueba, una vez finalizado el proceso de inducción.
Por otro lado, las reglas con factor de incertidumbre en su antecedente se pueden obtener por métodos clásicos si el factor de incertidumbre de cada atributo de entrada se expresa como un atributo más.
Respecto a la borrosidad, también existen sistemas que generan reglas borrosas: [Wang y Mendel, 92] , [González y Pérez, 95] , [Yeh y Chen, 96] , etc. aunque su aplicación se restringe a la lógica de proposiciones extendida. En estos sistemas se permite asignar valores borrosos a los atributos utilizados en las reglas inducidas.
Sin embargo, no existen sistemas que combinen la ILP con la lógica borrosa, para inducir reglas construidas mediante literales borrosos (predicados borrosos aplicados sobre variables). En una relación borrosa, la incertidumbre no se refiere necesariamente al valor de los atributos utilizados, sino, en general, a la pertenencia de sus tuplas a la misma (apartado A.3 ).
Por tanto, los sistemas existentes para "inducción de reglas borrosas" sólo son capaces de manipular un caso concreto de borrosidad (la que se refiere al valor de los atributos), y no relaciones borrosas generales, en las que la borrosidad va asociada a las tuplas y no a los atributos.
Con el sistema FZFOIL, que se describe a continuación, se permitirá utilizar como dato de entrada relaciones borrosas, en las que sus tuplas tengan asignado un grado de pertenencia, así como relaciones ordinarias. Por otro lado, las reglas que se induzcan serán definiciones borrosas, tanto de relaciones ordinarias como borrosas, construidas mediante literales borrosos u ordinarios. Estas reglas tendrán, además una medida de incertidumbre en forma de probabilidad, que indicará su precisión, útil para poder ser utilizada en la base de conocimiento de un sistema experto, por ejemplo.
El propósito de FZFOIL (FuZzy First Order Inductive Learner) es obtener una definición lógica de una relación P (fijada por el usuario), en función de otras relaciones Qi de la base de datos, de ella misma (permitiendo definiciones recursivas), e incluso de relaciones nuevas (inventadas por el sistema). Las relaciones de la base de datos pueden ser borrosas, y pueden venir definidas de forma extensional (por un conjunto de tuplas) o intensional (por una definición lógica).
Por tanto, se ha ampliado la potencia expresiva del sistema FOIL original ( [Quinlan, 90] ), tanto en la entrada de datos (datos borrosos, relaciones intensionales) como en la salida (definiciones con literales borrosos y con literales inventados).
Otra aportación interesante de FZFOIL es el empleo de la función Interés para evaluar literales, sustituyendo a la función Ganancia de FOIL, para corregir las deficiencias encontradas en esta última, explicadas en el apartado 3.2 . Además se han modificado los conjuntos locales de entrenamiento, empleando ahora proyecciones de los mismos sobre el conjunto inicial, para poder evaluar los literales candidatos con mayor precisión y obtener a la vez una medida de la calidad de la cláusula en construcción.
Las definiciones construidas están formadas por una cláusula de Horn o por la disyunción de varias de ellas. La forma general de cada una de estas cláusulas es la siguiente:
donde la cabeza de cada cláusula es siempre el predicado objetivo p con todos sus términos variables (X1,..., Xk), y el cuerpo lo forman una serie de literales (L1, L2,..., Ln). Estos literales son siempre:
Los literales pueden llevar el signo "¬" de la negación lógica.
A continuación se definen diferentes conceptos relacionados con la lógica borrosa. No han sido mencionados en el apartado 4.1 porque no son conceptos tan genéricos como los que definen la sintaxis o la semántica de la lógica borrosa de primer orden, sino que están más orientados a la inducción de conocimiento dentro de FZFOIL: literales borrosos, signo borroso, grado de cobertura, etc.
El nombre de una relación borrosa Q se denomina predicado borroso q, o dicho de otro modo, la interpretación del predicado borroso q es la relación borrosa Q.
Un literal borroso L es una fórmula atómica, formada por un predicado borroso q aplicado sobre términos variables:
Un literal borroso puede llevar el símbolo "¬" de la negación lógica.
Decimos que una cláusula de Horn (apartado 2.5.1) es borrosa cuando está construida con literales borrosos, bien en su cabeza (consecuente) o en su cuerpo (antecedentes) o en ambos.
Al definir relaciones ordinarias, se puede hablar del signo positivo o negativo de una tupla ( apartado 2.5.2.1 ), asociándolo a su pertenencia o no a la relación objetivo. Por el contrario, con relaciones borrosas, el concepto de signo positivo o negativo de una tupla pierde su significado original, ya que el conjunto de pertenencia (apartado A.1.1 ), deja de ser el par de valores {0, 1} para convertirse en el intervalo [0, 1].
Del mismo modo que existe un grado de pertenencia borroso a una relación borrosa, será necesario también borrosificar el concepto de signo de una tupla, para indicar su grado de pertenencia a la relación objetivo (borrosa).
Por similitud al caso booleano, definimos el signo borroso de una tupla t = <a1,..., ak>, y lo representamos como SB(t), como el grado con que t satisface ( apartado 4.3.2.3 ) al predicado objetivo p con las variables (V1,..., Vk) de la cabeza en una cláusula de Horn. También puede definirse como el grado de pertenencia de t a la relación objetivo P. Por tanto, el signo borroso tomará valores en el intervalo [0, 1]:
Si t es una tupla de una relación borrosa P, definimos el signo borroso de una tupla t', extensión suya (apartado 2.5.2.2 ) como el signo borroso de t:
Podemos definir un subconjunto de tuplas positivas (con signo "+") para una relación borrosa con las tuplas cuyo signo borroso sea exactamente igual a 1:
del mismo modo, las tuplas negativas (con signo "-") serán aquéllas cuyo signo borroso sea exactamente igual a 0 (al igual que en el caso booleano, estas tuplas pueden venir explícitamente declaradas u obtenerse por la suposición de mundo cerrado):
El conjunto de entrenamiento T para inducir una definición de una relación borrosa será un conjunto ordinario (
apartado 4.3.3.4
), formado por los subconjuntos de tuplas definidos anteriormente: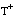 
, 
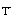y 
. Estos subconjuntos definen una partición de T:
Decimos que una tupla t satisface en grado 
un literal borroso L = q(V1,..., Vn), o que L se satisface en grado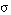 
para t, y lo expresamos como 
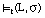, cuando al asignar a las variables (V1,..., Vn) de L los valores de la tupla t obtenemos una nueva tupla t' cuyo grado de pertenencia a Q es 
:
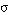El grado en que una tupla satisface a los antecedentes de una cláusula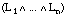 
lo definimos como el mínimo de los grados de satisfacción para cada uno de ellos:
Decimos que una tupla t satisface en grado 
una cláusula C = [L0 :- L1,..., Ln], o que C se satisface en grado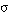 
para t, y lo expresamos como 
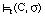, cuando t satisface en grado 
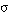la sentencia: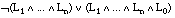 
Obsérvese que estas definiciones son coherentes con las dadas en el apartado 4.1 .
Una cláusula de Horn C = [L0 :- L1 ... Ln] cubre en grado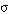 
a una tupla t cuando ésta satisface en grado 
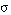a sus antecedentes:
El conjunto cubierto por una cláusula C será un conjunto borroso, que denominaremos TC(C), formado por todas las tuplas del conjunto de entrenamiento T cubiertas en algún grado por C. El grado de pertenencia de una tupla t al conjunto cubierto por C, es decir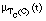 
, viene dado por el grado 
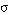en que C cubre a t:
Decimos que una cláusula C cumple la condición de k-cobertura o cobertura borrosa respecto de una tupla t cuando se cumple que:
es decir, cuando el grado con que C cubre a t es al menos k veces el grado con que t pertenece a la relación objetivo, siendo k el parámetro de k-cobertura.
La condición de k-cobertura se usa para determinar cuándo debe eliminarse una tupla t del conjunto de entrenamiento inicial T, tras finalizar la construcción de una cláusula C ( apartado 4.3.3.5 ).
Al definir esta condición en función del signo borroso de la tupla, se obliga a que los mejores ejemplos de la relación objetivo deban ser cubiertos en mayor grado que los menos buenos (tuplas con signo borroso menor).
En el caso de conjuntos ordinarios, la condición de k-cobertura se reduce a la cobertura ordinaria para el valor k = 1.
En la versión actual de FZFOIL, el valor de k-cobertura se ha definido como un parámetro de entrada, modificable por el usuario, que por defecto vale 0.8.
La relación residual asociada a una cláusula C la representamos como TR(C) y la definimos como el subconjunto de tuplas de P (relación objetivo) para las que no se cumple la condición de k-cobertura:
Decimos que una cláusula borrosa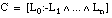 
es consistente sobre el conjunto T cuando se cumple la condición de consistencia borrosa, que definimos como:
Esta condición es una generalización de la consistencia booleana (EC. 2.12 ), de modo que cumple el principio de extensión para conjuntos borrosos (apartado A.1.3.7 ).
También se puede definir una k-consistencia para cláusulas borrosas, función del conjunto cubierto TC(C), de la relación objetivo P y del parámetro k, que toma valores en el intervalo [0, 1]:
Esta expresión es una extensión de la correspondiente a lógica booleana (EC. 2.15 ). Puede demostrarse (Apéndice B , apartado B.1 ) que la condición de k-consistencia no es más que una generalización de la consistencia, que se cumple para todas las cláusulas consistentes y algunas inconsistentes (las de precisión 3 igual superior a k). Para k = 1 ambas son equivalentes.
Del mismo modo se puede definir la k-consistencia de una definición D:
En la versión actual de FZFOIL, se aplica la condición de k-consistencia, siendo k un parámetro configurable por el usuario, y por defecto vale 0.9.
Pueden encontrarse otras definiciones para la consistencia en el caso de conjuntos borrosos, por ejemplo en [González y Pérez, 95] 4 :
Decimos que una cláusula borrosa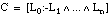 
es completa sobre el conjunto T cuando se cumple la condición de completitud borrosa, que definimos como:
Esta condición es una extensión borrosa de la completitud booleana (EC. 2.17 ).
También se puede definir una condición de k-completitud borrosa, en función del conjunto cubierto TC(C) y de la relación objetivo P, y de un parámetro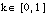 
.
Puede demostrarse que la condición de k-completitud borrosa es una generalización de la completitud borrosa, y que ambas son equivalentes para k=1.
También es sencillo demostrar que si una cláusula cumple la condición de k-cobertura respecto de todas las tuplas del conjunto T, entonces se cumple que C es k-completa sobre T (para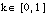 
):
Por tanto, es inmediato deducir que una condición suficiente (pero no necesaria) para que una cláusula sea k-completa es que la relación residual asociada ( apartado 4.3.2.5 ) sea vacía:
El recíproco no es cierto en general (a diferencia de lo que ocurre en el caso booleano, EC. 2.19 ), pues sólo se puede asegurar que la relación residual es vacía cuando se cumple la condición de completitud (o k-completitud para k=1):
Para una definición lógica borrosa D también se pueden definir las condiciones de completitud y k-completitud, para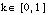 
:
En la actual versión de FZFOIL se aplica la condición de k-completitud, siendo k un parámetro configurable por el usuario que, por defecto, toma el valor 0.9.
En [González y Pérez, 95] puede verse otra definición de completitud borrosa, para finalizar la construcción de una definición. Se basa en la cardinalidad del corte-a (apartado A.1.4.3 ), tomando a como un umbral de cobertura mínima, aplicado sobre el conjunto de tuplas de P cubiertas por la última cláusula:
Al extender el concepto de pertenencia en una relación ordinaria por el de grado de pertenencia en una borrosa, se hace necesario borrosificar también otros conceptos, como el de longitud de descripción extensional para una relación borrosa.
Como vimos en el apartado 2.5.4.5 , la longitud de descripción extensional de una relación ordinaria Q se define como el número de bits necesarios para enumerar sus p tuplas en un conjunto de cardinalidad N (EC. 2.21 ); para ello, se informaba de:
Para el caso borroso se puede utilizar una definición similar que, además, incluya información sobre los grados de pertenencia de las tuplas a la relación Q:
podemos definir los conjuntos de tuplas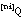 
, formados por las tuplas del conjunto universal que pertenecen a U con grado ni:
siendo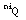 
el corte alpha (apartado A.1.4.3
) de Q para nivel ni.
Cada uno de los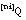 
se puede codificar (siguiendo un razonamiento similar al del caso de Q ordinaria) con:
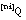, podemos descontar de N las tuplas consideradas en los subconjuntos anteriores; así, para codificar un 
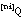cualquiera harán falta:
La expresión resultante para la longitud de descripción extensional de una relación borrosa Q, que representamos como LDE(Q), se calculará como la suma de las longitudes de descripción para los subconjuntos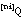 
. De todos los subconjuntos 
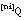sólo codificaremos aquellos que correspondan a tuplas con grado de pertenencia a Q distinto de cero, es decir, no hará falta codificar 
:
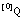Podemos comprobar que esta expresión es una extensión borrosa de
la EC. 2.21
, pues tomando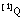 
como el subconjunto de tuplas "+" de una relación ordinaria, y 
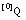como el de tuplas "-", coinciden ambas expresiones.
La longitud de descripción intensional de un literal borroso se puede definir de modo parecido a como se hizo para un literal ordinario (EC. 2.24 ):
donde el primer sumando indica la etiqueta lingüística ( apartado 4.3.4 ), el segundo el predicado (suponiendo que hay NR relaciones en la base de datos) y el último los argumentos del literal (suponiendo NA posibles argumentos). En el caso de literales ordinarios, las dos únicas etiquetas lingüísticas posibles (NE) son el signo afirmativo o negativo del literal.
Para cláusulas y definiciones borrosas, son aplicables las mismas expresiones para LDI indicadas en el caso booleano (EC. 2.25 y EC. 2.26 ).
Al igual que en FOIL, en FZFOIL se construyen las definiciones siguiendo un algoritmo formado por dos bucles:
También se utiliza un heurístico (tanto al construir definiciones como cláusulas) para limitar la complejidad de las descripciones, permitiendo la construcción de definiciones inconsistentes y/o incompletas. Este heurístico se basa en el principio de Mínima Longitud de Descripción de Rissanen (EC. 2.31 ).
Sin embargo, las diferencias en el algoritmo son numerosas ya que, al trabajar con lógica borrosa, ha sido necesario extender muchos de los conceptos utilizados en FOIL:
En el bucle externo de FZFOIL se construyen definiciones completas, formadas por una cláusula de Horn o por la disyunción de varias de ellas. En cada iteración del bucle se añade una nueva cláusula a la definición en construcción y se modifica el conjunto de entrenamiento, eliminando del mismo las tuplas cubiertas por la nueva cláusula. Esta idea es, esencialmente, la misma que se utiliza en otros algoritmos bien conocidos en el campo del aprendizaje, como el sistema AQ ( [Michalski, 87] ).
El algoritmo finaliza cuando se cumple la condición de k-completitud, concluyendo con una definición k-completa, o cuando se cumple la condición de poda por mínima longitud de descripción, y entonces la definición es incompleta.
Definición& FZFOIL (T +, T -, T ~, k-comp, k_cons, p, q1, q2,...)
Clausula Ci = construyeC (TRi - 1, T -, k_cons, p, q1, q2,...);
Di = Di-1 / Ci; /* añade cláusula k-consistente */
TCi = TCi - 1 » TC(Ci); /* actualiza TC */
hasta que (Di-1.es_Kcompleta(k_comp, TCi-1, P) || poda(Di-1, TCi-1));
El algoritmo finaliza cuando se cumple la condición de completitud borrosa, con una definición k-completa, o cuando se produce la poda por criterio de mínima longitud de descripción, resultando entonces una definición incompleta.
Las diferencias con el algoritmo basado en relaciones ordinarias (apartado 2.5.3.1 ) son:
ahora hay que aplicar la condición de k-cobertura para eliminar del conjunto inicial de entrenamiento las tuplas cubiertas por una cláusula.
En el bucle interno de FZFOIL (función construyeC en el pseudocódigo del bucle externo) se construyen cláusulas k-consistentes, cuyo consecuente es el predicado objetivo aplicado sobre variables, y cuyos antecedentes son literales construidos con predicados de la base de datos, o con predicados predefinidos (como la igualdad, comparación, etc. entre atributos).
En cada iteración del bucle interno se añade un nuevo antecedente a la cláusula y se modifica el conjunto de entrenamiento, seleccionando las tuplas que satisfacen el nuevo literal. La construcción de la cláusula finaliza cuando ésta es consistente o se cumple la condición de poda por mínima longitud de descripción (entonces se obtiene una cláusula inconsistente).
Clausula& construyeC (TR, T -, k_cons, p, q1, q2,...)
Clausula C0 = p; /* cláusula inicial = "p :- TRUE" */
Conjunto T1 = construyeT(TR) »; T -;
Literal Li = buscaAntecedente (Ti, p, q1, q2,...);
Ci = Ci-1 / (¬Li); /* añade antecedente Li */
Ti+1 = actualizarT (Ti, Li); /* tuplas que satisfacen Li */
hasta que (Ci - 1.es_Kconsistente(k_cons, TC, P) || poda(Ci - 1, T1));
Las diferencias respecto a la versión con relaciones ordinarias (apartado 2.5.3.2 ) son:
El objetivo de la función buscaAntecedente (ver pseudocódigo de apartado 4.3.3.2 ) es explorar el espacio de los literales candidatos y evaluarlos para elegir el mejor entre ellos.
Para medir la bondad de cada literal, Quinlan utiliza en FOIL un heurístico (Ganancia) basado en una medida de la información (EC. 2. 29 ). Sin embargo, este heurístico presenta algunas deficiencias en la evaluación de literales (apartado 3.2 ), por lo que en FZFOIL se ha preferido partir de otros heurísticos, basados en el interés de una regla (apartado 3.3 ), con los que se superan estos problemas.
Además, resulta más interesante que los argumentos de la función de evaluación no se midan en los conjuntos de entrenamiento locales (creados durante la construcción de una cláusula), sino en el conjunto inicial, ya que sólo de este modo se pueden prevenir algunos de los errores detectados (apartado 3.3.3 ). Por ello, se realizarán proyecciones de los conjuntos de entrenamiento locales sobre el conjunto inicial, de forma similar a como vimos para las relaciones ordinarias (figura 3.6 ).
Cada vez que se añade un nuevo literal Li a una cláusula en construcción Ci-1 se genera un nuevo conjunto de entrenamiento Ti+1, con las tuplas de Ti que satisfacen a Li. La proyección del nuevo conjunto Ti+1 sobre T1 la representamos como T1[i+1], y será siempre un subconjunto de T1[i] (proyección de Ti sobre T1):
Si alguno de los literales Li es borroso, el conjunto de entrenamiento local Ti+1 que se genera será también borroso. En este caso, la proyección de este conjunto (y de los posteriores) sobre T1, es decir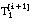 
, será también un subconjunto (borroso) de T1.
El interés de una cláusula debe ser máximo cuando el conjunto (borroso) cubierto por ella sea igual que la relación objetivo o, dicho de otro modo, cuando para cada tupla del conjunto cubierto coincidan su grado de pertenencia y su signo borroso. Por ello, es conveniente que la función de evaluación mida la correlación entre estos dos parámetros de cada tupla. Esto se puede conseguir modificando los argumentos de la función RI ( ), para conseguir una nueva función de evaluación que podemos llamar FRI (Fuzzy Rule Interest):
El conjunto de entrenamiento T que construye FOIL, para inducir una definición de una relación R ordinaria, está formado por dos subconjuntos: T +, con las tuplas que pertenecen a R (tuplas positivas o ejemplos), y T -, con las tuplas que no pertenecen a R (tuplas negativas o contraejemplos de R).
En el caso de FZFOIL, supondremos que el conjunto de entrenamiento inicial (T) es también un conjunto ordinario, pues realmente se define como el conjunto cubierto ( apartado 4.3.2.4 ) por la cláusula de Horn C0, sin literales negativos:
siendo L el literal construido para la relación objetivo R. Por tanto, T será un conjunto ordinario en el que todas sus tuplas tienen grado de pertenencia igual a 1. El signo de las tuplas dependerá de la relación objetivo R: si R es ordinaria, los signos serán "+" y "-"; en el caso borroso, tendrán signos borrosos.
En cualquier caso, podemos seguir considerando que los conjuntos T + y T - son subconjuntos de T, formados por las tuplas con signo borroso igual a 1 y 0 respectivamente:
Además, en el caso de una relación objetivo R borrosa, habrá que considerar también el subconjunto de tuplas con signo borroso distinto de 0 y de 1:
Por tanto, en el caso de relaciones borrosas, este conjunto de entrenamiento inicial (T) es un conjunto ordinario, al igual que en el caso de relaciones ordinarias.
Las tuplas negativas (conjunto T -) del conjunto de entrenamiento pueden venir explícitamente definidas, o ser construidas con la asunción de mundo cerrado (suponiendo que el grado de pertenencia de las tuplas que no aparecen en la relación R es cero).
Al igual que se hace en FOIL, además del conjunto de entrenamiento inicial T, se construyen una serie de conjuntos de entrenamiento locales, que denominaremos Ti, para evaluar los literales candidatos durante la construcción de las cláusulas (apartado 2.5.3.2 ). En el caso de relaciones borrosas, estos conjuntos locales serán borrosos, ya que aunque se construyen a partir del conjunto inicial T, sus tuplas se seleccionan de acuerdo con su grado de satisfacción ( apartado 4.3.2.3 ) a los literales antecedentes de la cláusula, como veremos más adelante.
La actualización de la relación residual asociada a la definición se realiza eliminando las tuplas del conjunto cubierto que cumplen la condición de k-cobertura.
Los conjuntos de entrenamiento posteriores Ti (para evaluar el resto de antecedentes de una cláusula) se construyen a partir del primero, modificando el grado de pertenencia de sus tuplas, y manteniendo el signo borroso de las mismas. El grado de pertenencia para una tupla se calcula como el mínimo entre el grado de pertenencia al conjunto anterior y el nivel en que satisface al literal candidato:
En FZFOIL se permite la construcción de definiciones con literales borrosos, tal como hemos visto en el apartado 4.3.3.3 , aplicando directamente sobre ellos la función de evaluación representada en [EC. 4.48] , que no es más que una generalización de la que se usaba en FOIL para literales ordinarios ( ).
Pero pueden obtenerse ventajas adicionales del uso de literales borrosos mediante la utilización de etiquetas lingüísticas ( ). Estas etiquetas actúan sobre un literal borroso como modificadores de su significado, entendiendo éste como el grado en que cada tupla lo satisface. Las etiquetas modifican el grado de satisfacción de las tuplas del conjunto de entrenamiento para el literal en cuestión, es decir, tienen un comportamiento similar al descrito en apartado 4.1.2.7 .
Las etiquetas aplicables sobre un literal borroso pueden ser:
Como ya hemos dicho, el resultado de aplicar una etiqueta lingüística sobre un literal borroso L, se refleja como una modificación del grado en que las tuplas del conjunto de entrenamiento lo satisfacen. Si denominamos h a la función de modificación asociada a una etiqueta H (generalmente h es de la forma
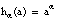, según
), el grado en que cualquier tupla t satisface al literal con etiqueta (que representaremos como HL) será:
Si nos fijamos en los parámetros de la función de evaluación usada en FZFOIL (
[EC. 4.48]
), podemos comprobar que los parámetros que se ven afectados por el uso de etiquetas lingüísticas en un literal borroso son NA y NAB, es decir, los que dependen del significado del literal borroso (a través del grado de pertenencia a 
según
EC. 4.54
y
EC. 4.55
). El nuevo valor de estos parámetros se calculará del mismo modo, pero modificando el grado de pertenencia al nuevo conjunto (resultado de aplicar
sobre
EC. 4.55
y
EC. 4.54
):
También tiene interés la aplicación de la negación lógica sobre literales borrosos con etiquetas lingüísticas. Así para un literal L podrían construirse, por ejemplo, los literales "no muy L", "no bastante L", "no algo L", etc. En este caso, el grado de satisfacción de una tupla t para la negación de un literal L con la etiqueta H (representado como ¬HL) se calculará como:
Por tanto, el resultado de permitir literales borrosos con etiquetas lingüísticas se traduce en una extensión del espacio de búsqueda de literales, a cambio de la posibilidad de construir mejores definiciones borrosas.
En la versión actual de FZFOIL se han implementado tres etiquetas lingüísticas, definidas del siguiente modo:
de modo que por cada literal borroso L sin etiquetas que se evalúe, se evaluarán 6 literales adicionales, resultantes de aplicar cada una de estas etiquetas sobre L (con los literales negados correspondientes). A continuación veremos un ejemplo en el que se aplican estas etiquetas.
Las relaciones intensionales son relaciones definidas por el usuario, pero que no son introducidas a través de su conjunto de tuplas, sino mediante una expresión lógica formada por una cláusula de Horn. Su aspecto es, por tanto, similar al de las definiciones lógicas inducidas por FZFOIL.
De este modo, es posible introducir fácilmente conocimiento de base en el sistema (ver nota a pie de ), construido a partir de las relaciones extensionales o de otras relaciones intensionales definidas previamente.
El consecuente de la cláusula que define una relación intensional es el predicado asociado a dicha relación, con todos sus atributos variables. Los antecedentes son literales correspondientes a:
Por ejemplo, dadas las relaciones extensionales de los matrimonios y de la relación hermanos, podríamos construir de forma intensional la relación binaria de los cuñados:
Veamos con un pequeño ejemplo el funcionamiento de la versión actual de FZFOIL. Supongamos una base de datos relacional en la que tenemos las siguientes relaciones:
Las tuplas en las que aparece el carácter ":" seguido de un número real entre 0 y 1 son tuplas de una relación borrosa ("enfermo", "fumador" y "barbudo" en este ejemplo); el número indica el grado de pertenencia a dicha relación.
Queremos inducir una definición para la relación borrosa "enfermo", usando para ello cualquiera de las relaciones (borrosas o no) de nuestra base de datos. En la versión original de FOIL, este ejemplo sólo podría ejecutarse para relaciones ordinarias, ya que no podríamos representar los diferentes grados de pertenencia de las tuplas. En nuestra versión, además, permitimos más matices (más flexibilidad) en la representación de las definiciones inducidas, al poder inventar nuevos predicados a partir de los existentes.
La definición que se induce (D1) está formada por la disyunción de dos cláusulas (C1 y C2):
Los números que aparecen en la primera línea indican:
Se puede observar que en la segunda cláusula se ha inventado un nuevo predicado, al añadir la etiqueta "bastante" al predicado borroso "fumador". De este modo, podemos leer la definición como: "una persona está enferma cuando es hija de otra que está enferma, o bien, cuando es bastante fumadora".
La introducción de relaciones intensionales, además de las relaciones extensionales, ofrece más potencia en la representación del conocimiento de base.
Pero la aportación más interesante de FZFOIL es la introducción de relaciones borrosas en la base de datos. Las relaciones borrosas usadas en FZFOIL permiten una descripción más precisa del mundo real, al poder representar la incertidumbre asociada a muchos aspectos de la realidad, al menos desde el punto de vista humano. Sentencias como
"si tienes mucho frío, es que tienes fiebre"
"si tienes fiebre y te duelen los huesos, es probable que tengas gripe",
son difícilmente inducibles a partir de una base de datos con relaciones ordinarias, pues, se pierde exactitud al representar conceptos borrosos como la sensación de dolor o de frío mediante relaciones ordinarias, a las que las tuplas pueden pertenecen o no, pero las que pertenecen lo hacen todas en la misma medida. Sólo con relaciones borrosas se puede cuantificar el grado de pertenencia de las tuplas.
Por otro lado, la posibilidad de inventar predicados añadiendo adverbios de cantidad como mucho, bastante, etc. a las relaciones borrosas ya existentes ofrece la flexibilidad necesaria para poder inducir en FZFOIL definiciones como las anteriores.
La adaptación del algoritmo FOIL para poder manejar relaciones borrosas ha requerido una serie de cambios, orientados al manejo de los grados de pertenencia de las tuplas a sus relaciones borrosas. Quizá los más significativos hayan sido los realizados en la función de evaluación de los literales candidatos, y la redefinición de conceptos como completitud, consistencia o cobertura para datos borrosos. Para la invención de predicados borrosos, a partir de otros ya existentes en los datos de partida, se han definido curvas de pertenencia para cada una de las etiquetas permitidas en los mismos, en función de los grados de pertenencia de las tuplas a los conjuntos borrosos.
1. Hay que observar que, cuando se habla de "conocimiento de primer orden", en realidad se está utilizando una elipsis de "conocimiento modelado con lógica de primer orden". Lo mismo ocurre con "conocimiento borroso de primer orden".
2. En nuestro desarrollo no utilizaremos el concepto de función borrosa, por ello evitaremos su definición en este punto. En caso necesario, podría extenderse la definición de función de la lógica de predicados (aplicación Un Æ U), para su versión borrosa en lógica borrosa de predicados.
De hecho, una de las limitaciones actuales de FOIL y de FZFOIL, es que no utilizan funciones en las definiciones lógicas que inducen. La utilización de funciones borrosas en FZFOIL se propone en el como posible futura mejora, para ampliar la capacidad expresiva del lenguaje de representación del conocimiento.
. 
;
[EC. 4.1]
[EC. 4.2]
, entonces
[EC. 4.4]
[EC. 4.5]
[EC. 4.6]
y 
[EC. 4.6]
y 
[EC. 4.7]
y 
[EC. 4.8]
y 
), entonces
[EC. 4.9]
si y sólo si la sentencia que está dentro del alcance del cuantificador se satisface en grado 
para una o más de las asignaciones de la variable cuantificada).
[EC. 4.11]
[EC. 4.12]
[EC. 4.13]
[EC. 4.14]
[EC. 4.15]
[EC. 4.16]
[EC. 4.17]
[EC. 4.18]
[EC. 4.19]
[EC. 4.20]
[EC. 4.21]
[EC. 4.22]
[EC. 4.23]
[EC. 4.24]
lo forma la unión de los conjuntos cubiertos por cada una de sus cláusulas:
[EC. 4.25]
[EC. 4.26]
[EC. 4.27]
[EC. 4.28]
[EC. 4.29]
[EC. 4.30]
[EC. 4.31]
[EC. 4.32]
[EC. 4.33]
[EC. 4.34]
[EC. 4.35]
[EC. 4.36]
[EC. 4.37]
[EC. 4.38]
[EC. 4.39]
[EC. 4.40]
, i={2...L}, 
[EC. 4.41]
, i={2...L}
el conjunto de niveles de Q
el conjunto ordinario de tuplas del nivel i-ésimo (ni) de Q
[EC. 4.42]
[EC. 4.43]
se construyen a partir del mismo.
[EC. 4.44]
[EC. 4.45]
[EC. 4.46]
[EC. 4.47]
[EC. 4.48]
cardinalidad del conjunto de entrenamiento T1
cardinalidad escalar (
)
suma de los signos borrosos de las tuplas del conjunto de entrenamiento T1
suma del mínimo entre signo borroso y grado de pertenencia al conjunto cubierto por la cláusula.
[EC. 4.49]
[EC. 4.50]
[EC. 4.51]
[EC. 4.52]
[EC. 4.53]
[EC. 4.54]
, en el caso general de que t se expanda en varias tuplas {t', t'',...} en Ti+1, se calculará como el máximo de los grados de pertenencia a Ti+1 de sus tuplas descendientes:
[EC. 4.55]
[EC. 4.56]
[EC. 4.57]
[EC. 4.58]
