4.8.2. Transformación en forma clausulada

1. Eliminación de todas las conectivas condicionales y bicondicionales mediante la equivalencia (9) y la definición del bicondicional. Esto es lo mismo que en lógica de proposiciones.
2. Introducción de negaciones mediante las equivalencias (1), (2) y (3) (como en lógica de proposiciones), y ahora también (11) y (12). Este paso se aplica sucesivamente hasta conseguir que los símbolos «¬» sólo afecten a átomos. Por ejemplo, si la sentencia original es:

   = (x)(¬(p(x) q(x)))

   el paso 1 nos permite obtener la sentencia equivalente:

   (x)(¬((¬p(x) q(x)) (¬q(x) p(x))))

   y el paso 2:

   (x)(¬(¬p(x) q(x)) ¬(¬q(x) p(x))) (por (3))

   (x)((¬¬p(x) ¬q(x)) (¬¬q(x) ¬p(x))) (por (2))

   (x)((p(x) ¬q(x)) (q(x) ¬p(x))) (por (1))

3. Independización de las variables cuantificadas, que consiste simplemente en cambiar los nombres de las variables que sean necesarios para que cada cuantificador se refiera a su propia variable. Por ejemplo,

   (x)(¬p(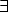x) (x)(q(x))) (x)(¬q(x) (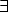y)(q(y)))

4. Eliminación de los cuantificadores existenciales mediante la regla de particularización de un existencial (Apartado 4.6.2), introduciendo las constantes y/o funciones de Skolem necesarias. Para el ejemplo anterior tendríamos:

   (x)(¬q(x) (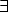y)(q(y))) (x)(¬q(x) q(f(x)))

5. Eliminación de los cuantificadores universales. En este momento, si se han seguido los pasos anteriores, sólo existen cuantificadores universales, y cada uno de ellos afecta a una variable diferente. Por tanto, podemos escribirlos todos al comienzo de la sentencia. Y, puesto que todas las variables están universalmente cuantificadas (como ya hemos dicho, sólo consideramos sentencias cerradas) podemos omitir la escritura de tales cuantificadores. No se trata, pues, en rigor, de «eliminarlos» sino de suponer que siempre existen.
6. Distribución de «» sobre «» . En el último ejemplo se ha llegado ya a una cláusula (disyunción de literales). Pero en general, tras el último paso tendremos una sentencia formada por literales unidos por las conectivas «» y «» de forma arbitraria. Lo mismo que hacíamos en lógica de proposiciones, aplicando la ley distributiva (4) llegaremos a una sentencia equivalente que sea una conjunción de cláusulas. Así, para el ejemplo que ilustraba el paso 2 tendremos:

   (p(x) ¬q(x)) (q(x) ¬p(x))

   ((p(x) ¬q(x)) q(x)) ((p(x) ¬q(x)) ¬p(x)) (por (4))

   (p(x) q(x)) ((¬q(x) q(x)) (p(x) ¬p(x)) (¬q(x) ¬p(x))) (también por (4))

   (p(x) q(x)) (¬q(x) ¬p(x))

   Para la última transformación se ha tenido en cuenta que p(x) ¬p(x) y ¬q(x) q(x) son sentencias válidas y por tanto pueden eliminarse de una conjunción (puesto que siempre se satisfacen).

7. Redenominación de variables para que cada cláusula tenga las suyas propias. En el último ejemplo resultan las cláusulas p(x) q(x) y ¬p(y) ¬q(y)

 DIT-ETSIT-UPM