 ,
,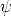 ,
, ,
,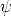 ,...} implica lógicamente una
sentencia
,...} implica lógicamente una
sentencia  si y sólo si toda interpretación que satisface al conjunto satisface también a
si y sólo si toda interpretación que satisface al conjunto satisface también a
 »
. Ahora hay que decir «toda interpretación y asignación de variables»
.
»
. Ahora hay que decir «toda interpretación y asignación de variables»
.
Lo mismo que allí, decir que  implica
implica 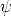 es lo mismo que decir el conjunto de
modelos de
es lo mismo que decir el conjunto de
modelos de 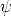 es un subconjunto del de
es un subconjunto del de  , y
, y  y
y 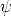 son equivalentes si y sólo si tienen el
mismo conjunto de modelos.
son equivalentes si y sólo si tienen el
mismo conjunto de modelos.
A las equivalencias que allí enumerábamos podemos añadir estas dos:
 x)(
x)( )
)  ¬(
¬(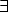 x)(¬
x)(¬ )
)
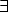 x)(
x)( )
)  ¬(
¬( x)(¬
x)(¬ )
)en las que se supone que  contiene a la variable libre x, y que ponen de manifiesto que
los cuantificadores universal y existencial no son independientes: lo que se expresa con
uno puede expresarse con el otro.
contiene a la variable libre x, y que ponen de manifiesto que
los cuantificadores universal y existencial no son independientes: lo que se expresa con
uno puede expresarse con el otro.
Hagamos un pequeño ejercicio de transformaciones sucesivas de una sentencia mediante la aplicación de estas equivalencias. Tomemos la sentencia que define recursivamente la relación «Superior» en función de la relación «Jefe» propuesta al final del Apartado 4.5.1. Para abreviar usaremos los símbolos j y s: I(s) = Superior, I(j) = Jefe:
( x)(
x)( y)((j(x,y)
y)((j(x,y)  (
(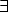 z)(j(x,z)
z)(j(x,z)  s(z,y)))
s(z,y))) 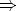 s(x,y))
s(x,y))
 (
( x)(
x)( y)(¬(
y)(¬(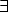 z)(j(x,z)
z)(j(x,z)  s(z,y))
s(z,y))  s(x,y)) (por (9))
s(x,y)) (por (9))
 (
( x)(
x)( y)((
y)(( z)(¬(j(x,z)
z)(¬(j(x,z)  s(z,y)))
s(z,y)))  s(x,y)) (por (12))
s(x,y)) (por (12))
 (
( x)(
x)( y)((
y)(( z)(¬j(x,z)
z)(¬j(x,z)  ¬s(z,y))
¬s(z,y))  s(x,y)) (por (3))
s(x,y)) (por (3))
 (
( x)(
x)( y)(
y)( z)(¬j(x,z)
z)(¬j(x,z)  ¬s(z,y)
¬s(z,y)  s(x,y)) (por asociatividad)
s(x,y)) (por asociatividad)
 (
( x)(
x)( y)(
y)( z)(¬(j(x,z)
z)(¬(j(x,z)  s(z,y))
s(z,y))  s(x,y)) (por (2))
s(x,y)) (por (2))
 (
( x)(
x)( y)(
y)( z)(j(x,z)
z)(j(x,z)  s(z,y))
s(z,y)) 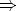 s(x,y)) (por (9))
s(x,y)) (por (9))
Tras estas prosaicas operaciones hemos llegado a un resultado interesante que, generalizándolo, podemos enunciar así: si una variable figura en el antecedente de un condicional y no en su consecuente, entonces es igual cuantificar la variable universalmente sobre el conjunto de la sentencia que cuantificarla existencialmente sobre el antecedente. Normalmente, la forma con cuantificación existencial se corresponde mejor con la expresión en lenguaje natural: en este ejemplo, «si existe algún individuo z tal que x es jefe de z y z es superior de y, entonces x es superior de y» .
La sentencia escrita en la quinta línea es la forma clausulada (Apartados 3.8.1 y 4.8.1)