 : (
: ( x)(pol(x)
x)(pol(x) 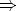 men(x))
men(x))
Habíamos visto que el conjunto de sentencias:
 : (
: ( x)(pol(x)
x)(pol(x) 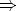 men(x))
men(x))
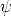 : (
: ( x)(men(x)
x)(men(x) 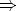 inf (x))
inf (x))
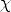 : pol(A)
: pol(A)
tiene un modelo mínimo: aquél en el que sólo el individuo representado por A está en las tres relaciones representadas por pol, men e inf. Pero también hemos visto que hay otros muchos modelos. Podemos incluir a cualquier otro en la relación inf (las tres sentencias se siguen satisfaciendo), o incluirlo en la relación men si además lo incluimos en inf.
En los sistemas deductivos con FOL puede adoptarse, como en la lógica de
proposiciones (Apartado 3.5.1), la asunción del mundo cerrado: si un átomo
terminal (o sea, que tiene todos sus términos asignados) no está incluido en 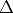 0,
ni tampoco está implicado por
0,
ni tampoco está implicado por 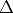 0, entonces es falso. Bajo esta asunción, el
modelo mínimo de las tres sentencias anteriores es también un modelo único. En
efecto, aunque aún no hemos llegado a los procesos deductivos en FOL, sí los
hemos estudiado en lógica de proposiciones (Apartado 3.7.1), y no es difícil
comprender que dadas las tres premisas anteriores sólo cabe deducir men(A) e
inf (A).
0, entonces es falso. Bajo esta asunción, el
modelo mínimo de las tres sentencias anteriores es también un modelo único. En
efecto, aunque aún no hemos llegado a los procesos deductivos en FOL, sí los
hemos estudiado en lógica de proposiciones (Apartado 3.7.1), y no es difícil
comprender que dadas las tres premisas anteriores sólo cabe deducir men(A) e
inf (A).
El suponer el mundo cerrado tiene también consecuencias para la representación del conocimiento normativo en FOL. Hasta ahora hemos escrito las definiciones intensionales de relaciones mediante sentencias bicondicionales. Por ejemplo, en la conceptuación del mundo de los bloques (Apartado 1.7) podemos definir la relación Bajo como la inversa de Sobre, lo que formalizaríamos así:
( x)(
x)( y)(bajo(x,y)
y)(bajo(x,y)  sobre(y,x))
sobre(y,x))
Pero para aplicar un razonamiento deductivo que permita, dada una situación definida por una extensión de la relación Sobre, obtener la extensión de la relación Bajo utilizamos solamente un sentido del bicondicional, es decir:
( x)(
x)( y)(sobre(x,y))
y)(sobre(x,y)) 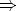 bajo(y,x))
bajo(y,x))
Ahora bien, en general, esta sentencia no puede considerarse una definición de Bajo, porque admite modelos en los que un objeto está bajo otro y sin embargo este otro no está sobre él. Por ejemplo, si I(sobre) = {(a,b)}, en el modelo mínimo de la sentencia debe ser I(bajo) = {(b,a)}, pero también sería un modelo aquél cuya interpretación de Sobre es la misma y la interpretación de Bajo es {(b,a), (b,c)}. Sin embargo, con la asunción de mundo cerrado el único modelo posible es el mínimo, y la sentencia condicional puede considerase una definición de la relación Sobre.
Lo mismo podemos decir de todas las definiciones intensionales. Así, la definición recursiva de Superior en función de Jefe (Apartado 4.3.1):
( x)(
x)( y)(superior(x,y)
y)(superior(x,y)  (jefe(x,y)
(jefe(x,y)  (
(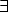 z)(jefe(x,z)
z)(jefe(x,z)  superior(z,y))))
superior(z,y))))
puede escribirse:
( x)(
x)( y)((jefe(x,y)
y)((jefe(x,y)  (
(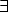 z)(jefe(x,z)
z)(jefe(x,z)  superior(z,y)))
superior(z,y))) 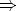 superior(x,y))
superior(x,y))