 x)(
x)( y)((y = encima-de(x))
y)((y = encima-de(x))  sobre(y,x))
sobre(y,x))
 x)(
x)( y)(libre(x)
y)(libre(x)  ¬(
¬(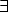 y)(sobre(y,x)))
y)(sobre(y,x)))
 x)(
x)( y)(más-arriba-que(x,y)
y)(más-arriba-que(x,y)  (sobre(x,y)
(sobre(x,y)  (
(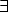 z)(sobre(x,z)
z)(sobre(x,z)  más-arriba-que(z,y))))
más-arriba-que(z,y))))En el mundo de los bloques vamos a utilizar estos símbolos:
Los axiomas del dominio que enunciábamos en lenguaje natural en el Apartado 1.7 se pueden representar con estas sentencias:
 x)(
x)( y)((y = encima-de(x))
y)((y = encima-de(x))  sobre(y,x))
sobre(y,x))
 x)(
x)( y)(libre(x)
y)(libre(x)  ¬(
¬(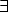 y)(sobre(y,x)))
y)(sobre(y,x)))
 x)(
x)( y)(más-arriba-que(x,y)
y)(más-arriba-que(x,y)  (sobre(x,y)
(sobre(x,y)  (
(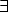 z)(sobre(x,z)
z)(sobre(x,z)  más-arriba-que(z,y))))
más-arriba-que(z,y))))
Otro ejemplo: el de los razonamientos sobre libros aburridos del Apartado 2.4.1, cuya conceptuación habíamos forzado en el Apartado 3.2 para formalizarlos en lógica de proposiciones. Los ejemplos eran:
y
Considerando como universo del discurso el conjunto de todos los libros, y denotando con los símbolos de predicado «ord» y «tab» las propiedades «ser un libro sobre ordenadores» y «ser tremendamente aburrido» , y con el símbolo de constante «E» el objeto «este libro» , el primer razonamiento se formaliza con estas tres sentencias:
 x)(ord(x)
x)(ord(x) 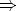 tab(x))
tab(x))
Y el segundo:
 x)(ord(x)
x)(ord(x) 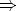 tab(x))
tab(x))