 si
si  se satisface
con esa I para todas las asignaciones posibles de sus variables; se escribe
«
se satisface
con esa I para todas las asignaciones posibles de sus variables; se escribe
« I
I »
. Una interpretación es un modelo de un conjunto de sentencias si es un modelo de
todas y cada una de ellas.
»
. Una interpretación es un modelo de un conjunto de sentencias si es un modelo de
todas y cada una de ellas.
Una interpretación I es un modelo de una sentencia  si
si  se satisface
con esa I para todas las asignaciones posibles de sus variables; se escribe
«
se satisface
con esa I para todas las asignaciones posibles de sus variables; se escribe
« I
I »
. Una interpretación es un modelo de un conjunto de sentencias si es un modelo de
todas y cada una de ellas.
»
. Una interpretación es un modelo de un conjunto de sentencias si es un modelo de
todas y cada una de ellas.
Ya hemos visto más arriba (Apartado 4.3.2) que la interpretación «natural» en la conceptuación de los «jefes» y «superiores» es un modelo de la sentencia
(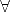 x)(
x)(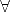 y)(jefe(x,y)
y)(jefe(x,y)  superior(x,y))
superior(x,y))
y también podríamos ver que es un modelo de la sentencia
(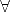 x)(
x)(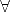 y)(
y)(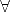 z)(jefe(x,z)
z)(jefe(x,z)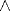 superior(z,y)
superior(z,y)  superior(x,y))
superior(x,y))
Otro ejemplo: consideremos una conceptuación con tres individuos, IndA, IndB, IndC y tres propiedades aplicables a estos individuos: ser político, ser mentiroso e ir al infierno. Formalizaremos los individuos con los símbolos «A» , «B» y «C» , de manera que, en las interpretaciones que podamos hacer, siempre será I(A) = IndA, I(B) = IndB, I(C) = IndC. Representaremos las propiedades con los símbolos de predicado (de grado 1) «pol» , «men» e «inf » . Sean las sentencias:
 : (
: (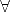 x)(pol(x)
x)(pol(x)  men(x))
men(x))
 : (
: (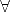 x)(men(x)
x)(men(x)  inf (x))
inf (x))
(«todos los políticos son mentirosos» y «todos los mentirosos van al infierno» ).
La interpretación I1 tal que:
I1(pol) = {IndA}
I1(men) = {IndA}
I1(inf ) = {IndA}
(«sólo el individuo IndA es político, mentiroso y va al infierno; los otros dos no tienen ninguna de esas propiedades» ) es un modelo de las sentencias. En efecto, para la asignación A(x) = IndA las dos sentencias se satisfacen, puesto que se satisfacen sus antecedentes (pol(A) y men(A)) y sus consecuentes (men(A) e inf (A)); para la asignación A(x) = IndB y para la asignación A(x) = IndC también se satisfacen, puesto ni los antecedentes ni los consecuentes se satisfacen.
La interpretación I2 tal que:
I2(pol) = {IndA}
I2(men) = {IndA,IndB}
I2(inf ) = {IndA,IndB,IndC}
(«IndA es político, mentiroso y va al infierno; IndB no es político, pero es mentiroso y
va al infierno; IndC no es político ni mentiroso, pero va al infierno»
) también es un modelo: para A(x) = IndA se satisfacen antecedentes y consecuentes
de  y
y  (luego ambas se satisfacen); para A(x) = IndB no se satisface el antecedente
de
(luego ambas se satisfacen); para A(x) = IndB no se satisface el antecedente
de  (luego
(luego  se satisface) y se satisfacen el antecedente y el consecuente de
se satisface) y se satisfacen el antecedente y el consecuente de  (luego
(luego
 se satisface); para A(x) = IndC no se satisfacen los antecedentes (luego
se satisface); para A(x) = IndC no se satisfacen los antecedentes (luego  y
y  se
satisfacen).
se
satisfacen).
Sin embargo, la interpretación I3 tal que:
I3(pol) = {IndA}
I3(men) = {IndA}
I3(inf ) = 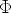
(«sólo el individuo A es político, sólo él es mentiroso, y nadie va al infierno»
; «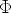 »
es la relación vacía) no es un modelo: para A(x) = IndA,
»
es la relación vacía) no es un modelo: para A(x) = IndA,  se satisface, pero no
se satisface, pero no  ,
porque su antecedente se satisface y no su consecuente.
,
porque su antecedente se satisface y no su consecuente.
Tampoco es un modelo la interpretación I4 tal que:
I4(pol) = {IndA}
I4(men) = 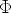
I4(inf ) = 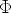
ya que en este caso se satisface  pero no
pero no  .
.
Se puede decir que las sentencias condicionales cerradas definen mundos
posibles: I1 e I2 son dos de los modelos de  y
y  , o mundos definidos por
, o mundos definidos por  y
y
 .
.
Supongamos que a  y
y  añadimos
añadimos
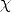 : pol(A)
: pol(A)
(un «hecho»
, conocimiento factual). I1 e I2 siguen siendo modelos de { ,
, ,
,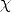 }, pero I1 es el
modelo mínimo. Un modelo es mínimo si ningún subconjunto de él es un modelo. Si
no hubiésemos añadido
}, pero I1 es el
modelo mínimo. Un modelo es mínimo si ningún subconjunto de él es un modelo. Si
no hubiésemos añadido 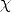 , el modelo mínimo sería I0 tal que I0(pol) = I0(men) =
I0(inf ) =
, el modelo mínimo sería I0 tal que I0(pol) = I0(men) =
I0(inf ) = 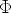 .
.