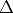 0
0 C existen algoritmos que demuestran C, y
C existen algoritmos que demuestran C, y
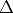 0
0 C y «no»
en el caso de que
C y «no»
en el caso de que 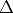 0 /
0 / C
C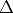 0
0 C existen algoritmos que demuestran C, y
C existen algoritmos que demuestran C, y
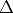 0
0 C y «no»
en el caso de que
C y «no»
en el caso de que 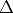 0 /
0 / C
C
Kurt Gödel demostró en 1930 el teorema de compleción para la lógica de predicados
de primer orden (otra cosa es su teorema de incompleción para los sistemas
axiomáticos de la aritmética). El teorema establece que si un conjunto de sentencias
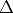 0 = {
0 = { 1,
1, 2,...
2,... n} implica lógicamente una sentencia C (
n} implica lógicamente una sentencia C (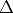 0
0 C) entonces existe
una demostración de C, es decir (Apartado 4.6.3), una secuencia finita, R, de
aplicación de reglas de inferencia que conduce de
C) entonces existe
una demostración de C, es decir (Apartado 4.6.3), una secuencia finita, R, de
aplicación de reglas de inferencia que conduce de 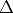 0 a C ({
0 a C ({ 1,
1, 2,...
2,... n}
n} RC).
RC).
Sin embargo, Alonzo Church demostró en 1936 que si no es el caso que 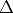 0
0 C
entonces no existe un procedimiento finito que permita demostrarlo (es decir, demostrar
que C no está implicada por
C
entonces no existe un procedimiento finito que permita demostrarlo (es decir, demostrar
que C no está implicada por 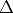 0). Por esto se dice que la lógica de predicados de primer
orden, en su forma general, es semidecidible (aunque hay formas particulares que sí son
decidibles, por ejemplo, aquella en la que los predicados sólo tienen uno o dos
argumentos).
0). Por esto se dice que la lógica de predicados de primer
orden, en su forma general, es semidecidible (aunque hay formas particulares que sí son
decidibles, por ejemplo, aquella en la que los predicados sólo tienen uno o dos
argumentos).