 x)(
x)( (x))
(x))
La regla de particularización de un universal permite razonar de lo general a lo particular:
P: ( x)(
x)( (x))
(x))
C:  (A)
(A)
Está basada en  ((
(( x)(
x)( (x))
(x)) 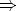
 (A)), donde
(A)), donde  (x) representa una sentencia que
contiene la variable libre x, y
(x) representa una sentencia que
contiene la variable libre x, y  (A) es la misma sentencia en la que x se ha sustituido
por una constante.
(A) es la misma sentencia en la que x se ha sustituido
por una constante.
Enseguida veremos que efectivamente se aplica en las demostraciones (de manera intuitiva cuando las demostraciones las hacemos mentalmente). En el modelo procesal de Prolog (Apartado A.3.2) ésta es la regla que se aplica cuando se sustituye una variable por una constante para unificar (o «ejemplarizar» ).