



A.5.5. La
negación en Prolog
Al final del Apartado A.4.4 vimos cómo puede definirse mediante dos reglas un
predicado que tiene éxito si otro fracasa y viceversa. Concretamente:
presente(X) :- ausente(X),!,fail.
presente(X).
|
Los procesadores de Prolog incorporan la operación not, que tiene este mismo
efecto, y que puede utilizarse en el cuerpo de las reglas:
presente(X) :- not(ausente(X)).
|
De este modo se libera la restricción sintáctica de que las reglas tengan que ser
cláusulas de Horn.
Ahora bien, la semántica de «not»
es procedimental y no coincide con la de «¬»
, y por eso recibe un nombre especial: negación como fracaso. Veámoslo con un
sencillo ejemplo.
La sentencia «(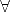 X)(¬p(X)
X)(¬p(X)  p(X))»
es equivalente a «(
p(X))»
es equivalente a «(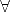 X)(p(X)
X)(p(X)  p(X))»
, y ésta es equivalente a «(
p(X))»
, y ésta es equivalente a «(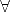 X)(p(X))»
. Es decir, equivale a afirmar que p(X) siempre es verdadera. Y eso está, naturalmente,
de acuerdo con la semántica de «¬»
’ y de «
X)(p(X))»
. Es decir, equivale a afirmar que p(X) siempre es verdadera. Y eso está, naturalmente,
de acuerdo con la semántica de «¬»
’ y de « »
, aunque parezca raro. Por ejemplo, si p representa «blanco»
la sentencia original dice que para todo objeto si ese objeto no es blanco entonces es
blanco. Supongamos que observamos un objeto blanco; ello no contradice a la sentencia
(y ésta se satisface). Pero si observamos un objeto de un color determinado entonces la
sentencia no se satisface (la observación corresponde a una interpretación que
no es un modelo de la sentencia). En otras palabras, todos los modelos de la
sentencia deben ser tales que los objetos son todos blancos. La sentencia es
pues, lógicamente, una manera extravagante de decir «todos los objetos son
blancos»
.
»
, aunque parezca raro. Por ejemplo, si p representa «blanco»
la sentencia original dice que para todo objeto si ese objeto no es blanco entonces es
blanco. Supongamos que observamos un objeto blanco; ello no contradice a la sentencia
(y ésta se satisface). Pero si observamos un objeto de un color determinado entonces la
sentencia no se satisface (la observación corresponde a una interpretación que
no es un modelo de la sentencia). En otras palabras, todos los modelos de la
sentencia deben ser tales que los objetos son todos blancos. La sentencia es
pues, lógicamente, una manera extravagante de decir «todos los objetos son
blancos»
.
La regla Prolog correspondiente sería: «p(X) :- not p(X).»
, y su lectura procedimental: «p(X) es verdadero si puede demostrarse que p(X) es falso
y viceversa»
. Pero esto es una contradicción, y no corresponde en absoluto a la semántica declarativa
del condicional y la negación.
No obstante, los resultados que se obtienen con la negación como fracaso suelen
coincidir con los que uno espera, si no se olvida la asunción del mundo cerrado.
Veámoslo con un ejemplo:
(1) (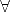 X)(llueve_en(X)
X)(llueve_en(X)  buena_cosecha(X))
buena_cosecha(X))
(2) (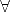 X)(¬llueve_en(X)
X)(¬llueve_en(X)  sube_turismo(X))
sube_turismo(X))
(3) (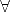 X)(buena_cosecha(X)
X)(buena_cosecha(X)  va_bien(X))
va_bien(X))
(4) (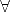 X)(sube_turismo(X)
X)(sube_turismo(X)  va_bien(X))
va_bien(X))
Es fácil ver que estas sentencias implican lógicamente va_bien(a), donde a es una
constante (país) cualquiera (es decir, (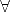 X)(va_bien(X))). Y, en efecto, esto es lo que se
obtiene con Prolog (es necesario añadir al menos un hecho, porque de lo contrario el
procesador da un error):
X)(va_bien(X))). Y, en efecto, esto es lo que se
obtiene con Prolog (es necesario añadir al menos un hecho, porque de lo contrario el
procesador da un error):
llueve_en(alemania).
buena_cosecha(X) :- llueve_en(X).
sube_turismo(X) :- not llueve_en(X).
va_bien(X) :- buena_cosecha(X).
va_bien(X) :- sube_turismo(X).
?- va_bien(alemania).
YES
?- va_bien(españa).
YES
|




 DIT-ETSIT-UPM
DIT-ETSIT-UPM
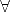 X)(¬p(X)
X)(¬p(X)  p(X))»
es equivalente a «(
p(X))»
es equivalente a «(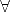 X)(p(X)
X)(p(X)  p(X))»
, y ésta es equivalente a «(
p(X))»
, y ésta es equivalente a «(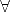 X)(p(X))»
. Es decir, equivale a afirmar que p(X) siempre es verdadera. Y eso está, naturalmente,
de acuerdo con la semántica de «¬»
’ y de «
X)(p(X))»
. Es decir, equivale a afirmar que p(X) siempre es verdadera. Y eso está, naturalmente,
de acuerdo con la semántica de «¬»
’ y de « »
, aunque parezca raro. Por ejemplo, si p representa «blanco»
la sentencia original dice que para todo objeto si ese objeto no es blanco entonces es
blanco. Supongamos que observamos un objeto blanco; ello no contradice a la sentencia
(y ésta se satisface). Pero si observamos un objeto de un color determinado entonces la
sentencia no se satisface (la observación corresponde a una interpretación que
no es un modelo de la sentencia). En otras palabras, todos los modelos de la
sentencia deben ser tales que los objetos son todos blancos. La sentencia es
pues, lógicamente, una manera extravagante de decir «todos los objetos son
blancos»
.
»
, aunque parezca raro. Por ejemplo, si p representa «blanco»
la sentencia original dice que para todo objeto si ese objeto no es blanco entonces es
blanco. Supongamos que observamos un objeto blanco; ello no contradice a la sentencia
(y ésta se satisface). Pero si observamos un objeto de un color determinado entonces la
sentencia no se satisface (la observación corresponde a una interpretación que
no es un modelo de la sentencia). En otras palabras, todos los modelos de la
sentencia deben ser tales que los objetos son todos blancos. La sentencia es
pues, lógicamente, una manera extravagante de decir «todos los objetos son
blancos»
.