




A.4.2. Un ejemplo: ordenación de listas
Este ejemplo empieza ya a alejarse del propósito inicial: presentar Prolog como un
lenguaje de representación del conocimiento basado en la lógica. La ordenación de
datos es un problema importante, tanto en la teoría como en la práctica de la
informática. Pero su inclusión aquí está justificada, sobre todo, porque ilustra muy
bien el hecho de que, con las implementaciones actuales de las «máquinas
lógicas»
, no podemos eludir el conocimiento del modelo procesal para diseñar programas
lógicos: veremos cómo el programa que se obtiene de una definición lógica es inviable
por su complejidad procesal, y cómo se pueden expresar en Prolog, declarativamente,
los principales algoritmos de ordenación.
Se trata de ordenar una lista de elementos. La lista resultante deberá tener el menor
de los elementos en la cabeza. Si los elementos son números, la relación de orden es
«=<»
(o «>=»
), ambas incluidas como predicados incorporados en Prolog, como ya sabemos. Si los
elementos son cadenas de caracteres se puede definir el orden aritmético, y utilizar las
reglas que ya vimos en el Apartado A.2. En los programas que vamos a desarrollar
utilizaremos los predicados «menor(X,Y)»
y «menorig(X,Y)»
. Si las listas son numéricas se sustituirán por «X<Y»
y «X=<Y»
, y si son alfabéticas, por las reglas que definen «menor_alf(X,Y)»
y «menorig_alf(X,Y)»
(Apartado A.2.5). O bien se añadirán las reglas:
menor(X,Y) :- X<Y.
menorig(X,Y) :- X=<Y.
|
en un caso, o
menor(X,Y) :- menor_alf(X,Y).
menorig(X,Y) :- menorig_alf(X,Y).
|
en el otro.
Ordenación mediante una definición lógica
Veamos, como elemento previo, la definición de un predicado que permite comprobar si
una lista está o no ordenada: «ordenada(X)»
deberá ser verdadero (o sea, «tener éxito»
) si la lista X está ordenada, y falso («fracasar»
) en caso contrario. Una lista vacía o que tiene un solo elemento está ordenada; si tiene
dos o más elementos estará ordenada si el primero es menor o igual que el
segundo y el resto de los elementos está ordenado. La traducción a reglas es
inmediata:
ordenada([]).
ordenada([X]).
ordenada([X,Y|L]) :- menorig(X,Y),ordenada([Y|L]).
|
Pasemos ya al problema de la ordenación de listas. Una definición totalmente
declarativa consiste en decir que L2 es una versión ordenada de L1 si L2 es una
permutación de L1 que está ordenada. Traduciéndola a una regla Prolog:
orden_log(L1,L2) :- permutacion(L1,L2),ordenada(L2).
|
Esta regla es perfectamente válida, y, acompañada de las que definen
«permutacion(X,Y)»
(Apartado A.2.3) y «ordenada(X)»
puede utilizarse para ordenar listas:
?- orden_log([3,2,1],X).
X=[1,2,3]
|
Pero hagamos la lectura procedimental. La regla dice que ante el objetivo definido
por esa consulta han de generarse los subobjetivos «permutacion([3,2,1],X)»
y «ordenada(X)»
. Con las reglas de «permutacion»
el procesador ensaya una primera unificación: [3,2,1]/X, pero como
«ordenada([3,2,1])»
fracasa, genera una segunda permutación y unifica [3,1,2]/X, con la que vuelve a
fracasar el segundo subobjetivo, y así hasta encontrar la «buena»
permutación: [1,2,3], que conducirá a la respuesta «X=[1,2,3]»
. En cualquier caso, el procesador sigue generando permutaciones (nosotros
sabemos que hay una sola respuesta, pero él no; luego veremos una manera de
«decírselo»
) hasta agotar todas las posibilidades. Con tres elementos sólo hay seis permutaciones,
pero si la lista tiene n elementos se generarán n × (n - 1) × (n - 2)... × 1 = n!
permutaciones. Una lista de diez elementos tiene 10! = 3.628.800 permutaciones, y una
de cien, 100! 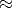 10158. Para hacernos una idea de lo que esto significa, supongamos que
el ordenador puede generar una permutación, y comprobar si está ordenada, cada
milisegundo. Para ordenar una lista de diez elementos con este procedimiento tardaría
10!/(1000 × 3600)
10158. Para hacernos una idea de lo que esto significa, supongamos que
el ordenador puede generar una permutación, y comprobar si está ordenada, cada
milisegundo. Para ordenar una lista de diez elementos con este procedimiento tardaría
10!/(1000 × 3600) 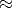 1 hora, y si la lista tiene cien elementos sería necesario un
número de años que en decimal habría que escribir con un 3 seguido de 147
dígitos.
1 hora, y si la lista tiene cien elementos sería necesario un
número de años que en decimal habría que escribir con un 3 seguido de 147
dígitos.
Así pues, si la definición es lógicamente intachable, procesalmente es desastrosa. En
efecto, «permutación(L1,L2)»
actúa como un «generador»
, y «ordenada(L2)»
como un «comprobador»
. El método que se aplica, interpretado procesalmente, es de «genera y comprueba»
, pero en este caso «genera»
es «genera todas y cada una de las permutaciones»
. Existen muchos algoritmos de ordenación, pero todos ellos comparten la idea de que
no es preciso generar a ciegas cualquier permutación, sino solamente aquellas que van
«mejorando»
progresivamente a la lista original. Veamos algunos de estos algoritmos y sus
traducciones a programas Prolog.
Ordenación mediante un algoritmo de selección
He aquí un algoritmo:
- Si la lista está vacía, o si contiene un solo elemento, entonces ya está ordenada. Si
no, considerar como «primer elemento»
de la lista al que figura en cabeza.
- Examinar todos los elementos que siguen al «primer elemento»
y seleccionar el menor de ellos; si éste es menor que el «primer elemento»
, intercambiarlos.
- Si el siguiente al «primer elemento»
(antes del intercambio) era el último de la lista, entonces la lista está ya ordenada.
Si no, considerar como «primer elemento»
ese elemento siguiente y volver al paso 2.
Comparando este algoritmo con el modelo procesal resultante de la definición
lógica, podemos observar que no genera todas las permutaciones posibles. En cada
momento, la lista está formada por dos partes, una ordenada y otra desordenada. Cada
vez que se ejecutan los pasos 2 y 3, un elemento de la parte desordenada se
intercambia, si es necesario, con el último de la parte ordenada; la parte ordenada
«crece»
mientras la desordenada «disminuye»
. De este modo, las permutaciones que se van generando van siendo sucesivamente
mejores. Si la lista tiene inicialmente n elementos completamente desordenados (es
decir, en orden inverso), sólo se generan n permutaciones. Para cada una de ellas, el
paso 2 del algoritmo implica una sucesión de operaciones de comparación con los
elementos de la parte desordenada. El número total de operaciones de comparación e
intercambio es: n + (n - 1) + (n - 2) + ... + 1 = n × (n + 1)/2, que, para n
grande, es del orden de n2 (y no de n!). Evidentemente, esto cambia las cosas.
Siguiendo con el ejemplo del subApartado anterior, si el ordenador realiza una
operación cada milisegundo, para diez elementos el tiempo de ordenarlos sería 102
milisegundos (una décima de segundo), y para cien elementos, 1002/1000 = 10
segundos.
Veamos cómo puede redefinirse en Prolog el predicado de ordenación (que ahora
llamaremos «orden_sel(L1,L2)»
) para que el proceso sea similar al descrito por el algoritmo. En primer lugar, y dado
que la definición va a ser recursiva, escribiremos una cláusula que permitirá
«cerrar»
la recursividad, expresando que la lista vacía está ordenada:
Con un predicado «perm_menor_cab(L1,L2)»
que se satisfaga si la lista L2 es igual al resultado de intercambiar la cabeza de L1 con el
menor de los elementos de su cola, podemos escribir la regla recursiva que define
«orden_sel»
:
R2: orden_sel(L,[M|Lord]) :-
perm_menor_cab(L,[M|Lprov]),
orden_sel(Lprov,Lord).
|
Esta regla reduce recursivamente el problema de ordenar una lista L al de obtener
una permutación de la misma, [M|Lprov], que sea igual al resultado de intercambiar el
menor elemento de L, M, con su cabeza y ordenar Lprov, hasta que Lprov sea
la lista vacía (y en ese momento el procesador de reglas y hechos utilizará
«orden_sel([],[]).»
. De este modo, el proceso que se genera es similar al bucle de los pasos «2»
y «3»
del algoritmo.
Pasemos ahora a definir «perm_menor_cab(L1,L2)»
, que corresponderá al paso «2»
del algoritmo, en el que implícitamente hay un bucle: la cabeza de L1 se va
comparando con el resto de elementos. Suponiendo que existen los predicados
«menor_cab(L)»
(que se satisface si L es una lista en la que ningún elemento es menor que la cabeza) y
«permuta_cab(L1,L2)»
(que se satisface si L2 es el resultado de intercambiar la cabeza de L1 con algún otro
elemento de L1 menor que esa cabeza), las reglas pueden ser:
R3: perm_menor_cab(L,L) :- menor_cab(L).
R4: perm_menor_cab([C|L],Lperm) :-
permuta_cab([C|L],Lperm),
menor_cab(Lperm).
|
«permuta_cab(L1,L2)»
puede definirse con una sola regla:
R5: permuta_cab([C|L],Lperm) :-
concatena(L3,[X|Resto],L),
menor(X,C),
concatena([X|L3],[C|Resto],Lperm).
|
Finalmente, «menor_cab(L)»
puede definirse así:
R6: menor_cab([]).
R7: menor_cab([X]).
R8: menor_cab([X,X1|L]) :-
menorig(X,X1),menor_cab(X|L).
|
Estas ocho reglas definen completamente el algoritmo en Prolog.
Ordenación mediante un algoritmo de inserción
El procedimiento de selección busca entre los elementos no ordenados de la lista y
selecciona el menor, para colocarlo al final de los elementos ya ordenados (todos
menores o iguales que él). El de inserción consiste en elegir el primero de los no
ordenados y buscar en la parte ordenada para insertarlo en el lugar que le corresponda.
Es decir:
- Si la lista está vacía, o si contiene un solo elemento, entonces ya está ordenada. Si
no, considerar como «primer elemento»
de la lista al que figura en cabeza. Sea Lord una lista inicialmente vacía.
- Insertar el «primer elemento»
en Lord, en el lugar que le corresponda.
- Si el «primer elemento»
es el último de la lista, la lista está ordenada. Si no, considerar como «primer
elemento»
el siguiente al que actualmente es el «primer elemento»
y volver al paso 2.
Suponiendo que existe un predicado «inserta(X,L,XenL)»
que se satisface cuando XenL es el resultado de insertar X en el lugar adecuado de L, la
definición del predicado para la ordenación es:
R1: orden_ins([],[]).
R2: orden_ins([X|L],XenLord) :-
orden_ins(L,Lord),
inserta(X,Lord,XenLord).
|
Y la definición de «inserta(X,L,XenL)»
:
R3: inserta(X,[],[X]).
R4: inserta(X,[Y|L],[Y|XenL]) :-
menor(Y,X), inserta(X,L,XenL).
R5: inserta(X,[Y|L],[X,Y|L]) :- menorig(X,Y).
|
Ordenación mediante un algoritmo de intercambio
Veamos ya muy brevemente el tercero de los algoritmos básicos de ordenación, dando
directamente su versión en Prolog. Es el conocido como «algoritmo de la
burbuja»
. En lugar de «inserta»
utiliza el predicado «burbuja(L,Lburb)»
, tal que Lburb es una permutación de L en la que todas las parejas de elementos
adyacentes de L que estaban en mal orden se han intercambiado:
R1: orden_bur(L,L) :- ordenada(L).
R2: orden_bur(L,Lord) :-
burbuja(L,L1),orden_bur(L1,Lord).
|
(Obsérvese que la primera regla incluye como caso particular «orden_bur([],[])»
. Aquí es preciso formular la regla más general, porque la regla recursiva no
va reduciendo, como ocurría en los algoritmos anteriores, la longitud de la
lista).
Y «burbuja»
puede definirse así:
R3: burbuja([],[]).
R4: burbuja([X],[X]).
R5: burbuja([X,Y|L],Lburb) :-
menorig(X,Y),
burbuja([Y|L],L1),
Lburb = [X|L1].
|
(X e Y están bien ordenados; la «burbuja»
se traslada a [Y|L]).
R6: burbuja([X,Y|L],Lburb) :-
menor(Y,X),
burbuja([X|L],L1),
Lburb = [Y|L1].
|
(X e Y se intercambian, y la «burbuja»
se traslada a [X|L]).
Ordenación mediante el algoritmo “quicksort”
Los tres algoritmos anteriores requieren un número de operaciones del orden (para n
grande) de n2, siendo n la longitud de la lista. Veamos, para completar, un algoritmo
mucho más rápido, llamado «quicksort»
, en el que el número de operaciones es del orden de n × log 2(n). Suponiendo una
operación cada milisegundo, el tiempo para ordenar diez elementos resulta ser unos
3 ms, y para cien elementos, unos 660 ms.
El algoritmo quicksort se basa en una operación, «partición»
, que consiste en repartir los elementos de la lista L en dos listas, L1 y L2,
tales que todo elemento de L, EL, esté en L1 si EL es menor o igual que M, o
en L2 si EL es mayor que M (donde M es un elemento arbitrario de L. (Para
conseguir el mejor comportamiento del algoritmo, M debería ser la mediana de los
elementos de L, pero no lo podemos calcular, porque el problema de encontrar
la mediana se remite al de ordenar los elementos). En las reglas que damos
se toma el primer elemento). Definida esta operación mediante el predicado
«particion(M,L,L1,L2)»
, el algoritmo consiste en hacer la partición y aplicarlo recursivamente a las dos listas
resultantes. Expresado con cláusulas:
R1: orden_qks([],[]).
R2: orden_qks([M|CL],Lord) :-
particion(M,CL,L1,L2),
orden_qks(L1,Lord1),
orden_qks(L2,Lord2),
concatena(Lord1,[M|Lord2],Lord).
|
Las cláusulas para «partición»
son:
R3: particion(X,[],[],[]).
R4: particion(M,[X|L],[X|L1],L2) :-
menor(X,M), particion(M,L,L1,L2).
R5: particion(M,[X|L],L1,[X|L2]) :-
menorig(M,X), particion(M,L,L1,L2).
|
Todos los programas desarrollados en este Apartado son declarativos. Pero, salvo el
primero («orden_log»
), se han obtenido a partir de un enfoque procedimental (o algorítmico) al problema.





 DIT-ETSIT-UPM
DIT-ETSIT-UPM
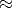 10158. Para hacernos una idea de lo que esto significa, supongamos que
el ordenador puede generar una permutación, y comprobar si está ordenada, cada
milisegundo. Para ordenar una lista de diez elementos con este procedimiento tardaría
10!/(1000 × 3600)
10158. Para hacernos una idea de lo que esto significa, supongamos que
el ordenador puede generar una permutación, y comprobar si está ordenada, cada
milisegundo. Para ordenar una lista de diez elementos con este procedimiento tardaría
10!/(1000 × 3600) 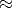 1 hora, y si la lista tiene cien elementos sería necesario un
número de años que en decimal habría que escribir con un 3 seguido de 147
dígitos.
1 hora, y si la lista tiene cien elementos sería necesario un
número de años que en decimal habría que escribir con un 3 seguido de 147
dígitos.