4.8.3 Aplicación de la regla de resolución

4.8.3. Aplicación de la regla de resolución

Como en lógica de proposiciones, la regla de resolución se aplica a dos cláusulas que compartan un literal con distinto signo, las generatrices, para dar lugar a una resolvente. Pero ahora hay un elemento nuevo: los literales no son simples variables proposicionales (con o sin la negación), sino átomos que contienen términos (constantes, variables o funciones). Esto hace necesaria hace necesaria una operación previa a la resolución, llamada unificación.

Dados dos literales con distinto signo, la unificación consiste en igualar sus argumentos, pero puede ocurrir que esto no esa posible, y en ese caso los literales no son unificables (y no se puede aplicar la resolución). Si uno de los literales (o ambos) contiene sólo variables entonces la unificación siempre es posible. Por ejemplo, p(x,y) y ¬p(A,z) son unificables: basta sustituir en el primero la variable x por la constante A y la variable y por la variable z. Abreviadamente, lo representaremos con la notación: «{A/x,z/y}» . Estas sustituciones deberán trasladarse a la resolvente. Obsérvese que lo que se ha hecho es aplicar la regla de inferencia de particularización de un universal (Apartado 4.6.1).

Otro ejemplo: la versión con resolución de uno de los razonamientos del Apartado 4.6.3 es:

P1: ¬ord(x) $\/$ tab(x)

P2: ord(E)

C: tab(E)

El literal ¬ord(x) se ha unificado con ord(E) mediante la sustitución de la variable x por la constante E, es decir, {E/x}.

Un ejemplo más:

P1: ¬p(A,x) $\/$ q(x,B)

P2: p(A,C)

C: q(C,B) (unificación: {C/x})

Pero si P2 fuese, por ejemplo, p(B,C), la unificación sería imposible (A y B son constantes diferentes que no pueden unificarse).

La presencia de funciones en el lenguaje hace que en la práctica los algoritmos de unificación sean complejos, pero ya no entraremos en ese nivel de detalle, que conceptualmente no es muy importante.

Sí parece importante señalar un resultado que justifica teóricamente el uso de constantes y funciones de Skolem. Recordemos (Apartado 3.7.1) que llamábamos 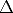₀ al estado inicial del proceso deductivo, formado por el conjunto de premisas (axiomas del dominio y hechos) y, si se utiliza refutación, también la conclusión negada. Sea 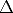₀^fc el resultado de convertir todas las sentencias a su forma clausulada, y supongamos que en esta transformación se han introducido constantes o funciones de Skolem. Como vimos en el Apartado 4.6.2, al hacerlo se utiliza la que hemos llamado «regla de particularización de un existencial» , que está basada en un falso teorema. De aquí que en realidad, 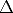₀^fc no es equivalente a 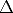₀. Sin embargo, el resultado a que nos referimos es un teorema:

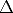₀ es insatisfactible si y sólo si 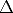₀^fc es insatisfactible.

DIT-ETSIT-UPM

Portada