 Apéndice A :
Apéndice A :

 Conceptos de lógica borrosa
Conceptos de lógica borrosa



El término "lógica borrosa" (fuzzy logic) puede interpretarse como ( [Kantrowitz et al., 94] ) un superconjunto de la tradicional lógica booleana, que ha sido extendida para manejar el concepto de "parcialmente verdadero" (valores de verdad entre "absolutamente verdadero" y "absolutamente falso") 1 . Fue presentada por Lotfi Zadeh de UC/Berkeley en los años 60 ( [Zadeh, 65] , [Zadeh, 73] ), como un medio para modelar la incertidumbre del lenguaje natural.
Según Zadeh , no debería considerarse la teoría borrosa como una simple teoría, sino que se debería considerar el proceso de borrosificación (en inglés fuzzification) como una metodología para generalizar cualquier teoría desde su versión ordinaria (discreta) a una nueva versión continua (borrosa) (véase el principio de extensión, apartado A.1.3.7 ). Así puede hablarse de "cálculo borroso", "ecuaciones diferenciales borrosas", "autómatas borrosos" ( [Klir y Yuan, 95] ), "sistemas dinámicos borrosos", etc.
Del mismo modo que se verifica una estrecha relación entre la lógica booleana y el concepto de subconjunto, así también se cumple una relación similar entre la lógica borrosa y la teoría de conjuntos borrosos ( apartado A.1 ).
En la teoría clásica de conjuntos, dado un elemento x de un universo U y un subconjunto ordinario A Õ U, puede definirse una función característica cA que define qué elementos de U pertenecen al conjunto A y cuáles no ( [Klir y Yuan, 95] ), del siguiente modo:
de este modo, la función característica de A asigna a cada elemento de U, un elemento del conjunto {0, 1}:
La función característica cumple las siguientes propiedades para la complementación, intersección y unión de conjuntos:
cA»B(x) = cA(x) + cB(x) (suma lógica)
Para un universo U se define un subconjunto borroso A de U como un conjunto de pares de la forma:
A = { <x, mA(x)> }, "x U[EC. A.3]
donde mA(x) es una función de pertenencia que toma sus valores en un conjunto M , llamado conjunto de pertenencia, que generalmente es el intervalo cerrado de reales entre 0 y 1:
Por tanto, la función de pertenencia de un conjunto borroso A no es más que una extensión de la función característica definida para conjuntos ordinarios ( [EC. A.2] ), ya que si se hace M = {0, 1}, entonces A se reduce a un subconjunto ordinario (la teoría clásica de conjuntos es un caso particular de la teoría de conjuntos borrosos):
En la literatura se suelen emplear dos notaciones distintas para la función de pertenencia de un conjunto borroso:
de modo que se usa un mismo símbolo tanto para denominar al conjunto borroso como para su función de pertenencia; según indican ( [Klir y Yuan, 95] ), no existe ambigüedad en este doble uso del mismo símbolo: cada conjunto borroso queda completa y unívocamente definido por una función de pertenencia, por lo que los símbolos de las funciones de pertenencia podrían también usarse en los conjuntos borrosos asociados.
Dado que una relación biunívoca no es necesariamente una identidad (en sentido matemático), no exime de ambigüedad, por lo que utilizaremos la primera notación: A para el subconjunto borroso y mA para su función de pertenencia.
Se definen las relaciones de igualdad e inclusión entre dos subconjuntos borrosos A y B del siguiente modo:
La intersección de conjuntos borrosos se define del siguiente modo 2 :
Se define el producto cartesiano entre conjuntos borrosos del siguiente modo:
A ¥ B = {< (a, b), min(mA(a), mB(b))>} [EC. A.14]
Por lo tanto, es un subconjunto borroso del producto cartesiano de los universos UA y UB .
El principio de extensión para conjuntos borrosos ( [Klir y Yuan, 95] ) establece que, para cualquier función ordinaria f : X Æ Y, pueden inducirse dos funciones de la siguiente forma:
m f(A)(y) = max { mA(x) f(x) = y}, "A F (X)
m f -1(B)(x) = mB(f(x)), "B F (Y)
donde F (X) y F (Y) son los conjuntos de todos los subconjuntos borrosos (fuzzy power sets) de X e Y respectivamente.
Se suele usar el mismo símbolo f, para la función ordinaria (en los universos X e Y) y para su extensión borrosa (en los universos F (X) y F (Y)).
Según este principio, tanto las relaciones de igualdad e inclusión como las operaciones de complementación, intersección y unión definidas para conjuntos borrosos se reducen a las definiciones clásicas en conjuntos ordinarios (para M = {0, 1}). Del mismo modo, todas las propiedades de estas operaciones en los conjuntos ordinarios (asociatividad, distributividad, etc.) se siguen cumpliendo en los conjuntos borrosos, excepto dos de ellas:
Se define el soporte (support) de un conjunto borroso A en el conjunto universal U , como el conjunto ordinario formado por todos los elementos de U cuyo grado de pertenencia en A es distinto de cero:
Se define la altura (height) de un conjunto borroso A como el mayor grado de pertenencia de todos los elementos en dicho conjunto:
Un corte alpha ( a-cut ) de un conjunto borroso A es un conjunto ordinario aA formado por todos los elementos del conjunto universal U cuyos grados de pertenencia en A son mayores o iguales que el valor a :
La utilidad de un conjunto borroso para modelar un concepto o una etiqueta lingüística dependerá de la forma que tome su función de pertenencia. Por ello, resulta de gran importancia la determinación práctica de una función de pertenencia precisa y justificable. Los métodos más usados son empíricos y se basan en experimentos realizados en una población, para medir la percepción subjetiva de los grados de pertenencia a la clase conceptual que se quiere modelar. Existen varios métodos:
A los conjuntos borrosos en los que la función de pertenencia asigna a sus elementos valores de pertenencia que son números reales, se les denomina conjuntos borrosos de tipo 1 . Es posible extender el concepto de conjunto borroso a los grados de pertenencia para construir así conjuntos borrosos de tipo 2, en los que los grados de pertenencia de sus elementos serían, a su vez, conjuntos borrosos. Aplicando de forma recursiva esta idea, se podrían construir, de forma general, conjuntos borrosos de tipo L . Por ejemplo, si definimos el concepto "inteligente" como un conjunto borroso de tipo 1, asignaríamos a cada persona un grado de pertenencia que sería un número real (por ejemplo, su cociente intelectual normalizado). Pero si definimos el concepto "inteligente" como un conjunto borroso de tipo 2, entonces el grado de pertenencia asignado a cada persona sería a su vez un conjunto borroso (por ejemplo, las etiquetas "superdotado", "por encima de la media", "normal", "por debajo de la media", "idiota", etc.).
Una relación representa una conexión o correspondencia entre dos o más elementos. Una relación ordinaria representa la existencia o ausencia de una asociación, interacción o interconexión entre los elementos de dos o más conjuntos. Este concepto se puede generalizar para permitir diversos grados de fuerza en la relación entre elementos. Los diferentes grados de asociación pueden representarse mediante grados de pertenencia a una relación borrosa, del mismo modo que el grado de pertenencia de un elemento a un conjunto borroso.
Por analogía, así como un conjunto ordinario puede verse como un caso particular de un conjunto borroso, una relación ordinaria puede considerarse como un caso particular de relación borrosa.
Una relación ordinaria entre dos conjuntos A y B se define por el conjunto de pares ordenados (a,b) que la verifican:
R = { (a, b) }, a A, b B[EC. A.22]
La relación así definida es binaria, aunque el mismo concepto se puede generalizar para formar relaciones de orden n , definidas por conjuntos de tuplas de grado n .
Se puede observar que una relación no es más que un subconjunto del producto cartesiano de los conjuntos que intervienen:
R Õ A1 ¥ A2 ¥ ... ¥ An[EC. A.23]
donde U = A1 ¥ A2 ¥ ... ¥ An representa el conjunto universal o universo del discurso para R. Debido a que una relación es realmente un conjunto, conceptos como inclusión, unión, intersección y complemento de conjuntos pueden ser aplicados directamente a relaciones.
Se dice que la relación R es ordinaria (no borrosa) cuando el conjunto de tuplas que la define es un subconjunto ordinario (no borroso) del producto cartesiano, con independencia de si los conjuntos Ai son ordinarios o borrosos.
Por ejemplo, para las relaciones de igualdad e inclusión entre conjuntos borrosos, definidas en el apartado A.1.2 , dados dos subconjuntos borrosos, A y B, se cumple que:
Por tanto, a pesar de que estas relaciones están definidas sobre conjuntos borrosos, no son borrosas.
De modo similar, podemos definir una relación borrosa R como un subconjunto (borroso) de las tuplas de U, es decir, en el que cada tupla tiene asociado un grado de pertenencia a R:
R Õ A1 ¥ A2 ¥ ... ¥ An[EC. A.24]
correspondiendo en este caso el signo "Õ" a la operación de inclusión entre conjuntos borrosos ( apartado A.1.2 ).
Se define una función de pertenencia, que expresa el grado de pertenencia de cada tupla t a la relación R, o dicho de otro modo, la fuerza de la relación R existente entre los atributos de t. El grado de pertenencia a una relación borrosa puede tomar valores en el intervalo [0, 1]:
La relación borrosa R se puede definir extensionalmente como el conjunto de pares de la forma:
R = {<t, mR(t)> | t U, mR(t) [0, 1]}[EC. A.25]
siendo t una tupla del conjunto universal U, y mR(t) el grado de pertenencia 4 de t a R.
Una relación borrosa R entre dos conjuntos ordinarios A y B se define como un conjunto de pares ordenados (a, b) , cada uno con un determinado grado de pertenencia mR a la relación R:
R = {<(a, b), mR(a, b)>}, a A, b B, mR [0, 1][EC. A.26]
donde mR indica en qué grado, o con qué intensidad, los elementos a y b están en la relación R. Una forma de representar una relación binaria borrosa es mediante la matriz de pertenencia, como veremos en el siguiente ejemplo ( [Fernández y Sáez-Vacas, 95] ):
La relación que existe entre las estaciones del año y la sensación de calor o frío que se siente es una relación borrosa (pues representa una relación subjetiva). Una persona podría expresarla explícitamente como:
A = {primavera, verano, otoño, invierno}
Del mismo modo que ocurre con las relaciones ordinarias, el concepto de relación borrosa se puede generalizar a órdenes superiores (entre más de dos conjuntos).
Se puede observar que la relación borrosa R no es más que un subconjunto borroso del producto cartesiano de A y B :
y, en general, una relación borrosa n-aria entre n conjuntos ordinarios: A1 , A2 ,..., An será un subconjunto borroso del producto cartesiano de todos ellos:
R Õ A1 ¥ A2 ¥ ... ¥ An[EC. A.27]
Al ser los conjuntos Ai ordinarios, su producto cartesiano consta de todas las tuplas ( a1 , a2 ,..., an) , y la relación borrosa R le asigna un grado de pertenencia a cada una de ellas.
Una relación borrosa entre dos conjuntos borrosos A y B se define como:
R = { <(a, b), mR(a, b)> }[EC. A.28]
a A, b B, mR(a, b) £ min(mA(a), mB(b))
que no es más que un subconjunto de su producto cartesiano ( apartado A.1.3.6 ). Cualquier subconjunto de A ¥ B será una relación borrosa entre ambos. La generalización al caso n-ario es inmediata:
Sean dos relaciones binarias R1 y R2, definidas entre los conjuntos A y B, y B y C respectivamente:
R1 = {<(a, b), mR1(a, b)>}, a A, b B
R2 = {<(b, c), mR2(b, c)>}, b B, c C
Se define la relación compuesta de R1 y R2 del siguiente modo:
R1 ° R2 = {<(a, c), maxb[min(mR1(a,b), mR2(b,c)))]}[EC. A.30]
es decir, para cada valor de b B se toma el mínimo de las funciones de pertenencia a las relaciones R1 y R2 de las parejas (a,b) y (b,c) respectivamente; el máximo de todos ellos es el grado de pertenencia a R1 ° R2 de la pareja (a,c).
La principal diferencia entre las proposiciones construidas en la clásica lógica booleana y las proposiciones borrosas está en los grados de verdad que se asignan a las mismas, dados por la función de evaluación E. En el caso booleano, una proposición p puede ser verdadera o falsa únicamente, representando estos valores como E(p) = 1 (verdadera) y E(p) = 0 (falsa). En el caso borroso, la función de evaluación puede tomar valores en el intervalo unidad:
Veremos a continuación cuatro tipos de proposiciones borrosas ( [Klir y Yuan, 95] ):
La forma canónica de una proposición borrosa p de este tipo es la siguiente:
siendo X una variable que toma valores x en algún conjunto universal U, y B es un subconjunto borroso definido en U.
El grado de verdad asociado a la proposición p se interpreta como el grado de pertenencia al conjunto borroso B. Así para un valor concreto x de la variable X, se tiene que
siendo E() la función de evaluación para las proposiciones.
En algunas proposiciones borrosas, los valores de la variable X son asignados a individuos de un conjunto I; en ese caso, la variable X se transforma en una función X: I Æ U, quedando la definición de la proposición borrosa ( [EC. A.32] ) como:
p: X(i) es B, siendo i I[EC. A.34]
Por ejemplo, si I es el conjunto de personas, cada persona está caracterizada por su edad, y está definido el conjunto borroso Joven, podemos representar la proposición "i es joven" como:
El grado de verdad de esta proposición vendrá dado por el grado de pertenencia al conjunto Joven para la edad de cada individuo:
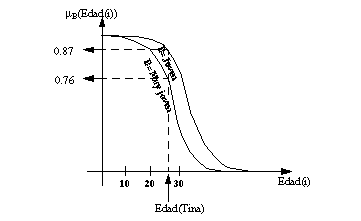
Por ejemplo, en la figura A-2 se define, para una edad de 25 años, un grado de pertenencia de 0.87 al conjunto borroso Joven.
Podemos distinguir dos tipos de proposiciones borrosas calificadas, dependiendo del tipo de calificador o modificador que se utilice:
La forma canónica de una proposición p de este tipo es la siguiente:
donde X es una variable que toma valores en un conjunto universal U, B es un subconjunto borroso definido en U, y V es un calificador borroso de verdad.
Definimos un calificador borroso de verdad V como una función que modifica el grado de verdad de una proposición borrosa p. El grado de verdad E(p) de la proposición p con calificador borroso de verdad se calcula como el resultado de aplicar una función V, que representa al calificador, sobre el grado de pertenencia al conjunto borroso B:
E(p) = V(mB(x)), "x U[EC. A.36]
Los calificadores borrosos de verdad son etiquetas lingüísticas aplicadas a los valores de verdad, por ejemplo: "verdadero", "muy verdadero", "algo verdadero", "muy falso", etc. y las funciones asociadas pueden verse en la figura A-1 .
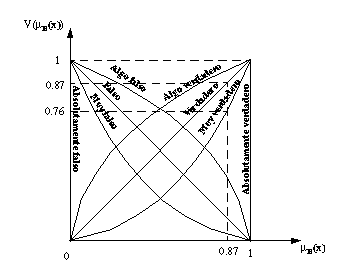
Los calificadores borrosos de verdad definen valores de verdad lingüísticos, que representan subconjuntos borrosos dentro del conjunto de pertenencia [0, 1]:
V {verdadero, falso, no verdadero, no falso, bastante verdadero, bastante falso,
poco verdadero, poco falso, muy verdadero, más o menos verdadero, ...}
Por ejemplo, la proposición borrosa "Tina es joven" se puede considerar que equivale a "Tina es joven es verdadero". Si suponemos que Tina pertenece al conjunto representado por el predicado joven con un grado de pertenencia de 0.87, entonces el grado de verdad de la proposición "Tina es joven" será también 0.87 ( figura A-1 ).
Pero podríamos construir otras proposiciones como "Tina es joven es muy verdadero", "Tina es joven es bastante verdadero", etc. cuyos grados de verdad ya no coinciden con el grado de pertenencia de Tina al conjunto joven, ya que los cualificadores borrosos "muy verdadero", "bastante verdadero", etc. afectan al significado de la proposición inicial "Tina es joven". Si modificaramos directamente los predicados "muy joven", "bastante joven", etc. obtendríamos proposiciones ("Tina es muy joven", "Tina es bastante joven", etc.) cuyos grados de verdad habrían cambiado del mismo modo ( figura A-2 ).
Una proposición borrosa sin calificador puede considerarse como un caso particular de proposición borrosa calificada, en el que el calificador corresponde a la etiqueta "verdadero", representada por la función S igual a la identidad.
La forma canónica de una proposición borrosa p de este tipo es la siguiente:
donde X es una variable que toma valores x en un conjunto universal U, B es un subconjunto borroso definido en U, P es un calificador borroso de probabilidad, y Pro(X es B) es la probabilidad del del evento borroso "X es B".
Las proposiciones borrosas de este tipo describen restricciones en las distribuciones de probabilidad en el universo U. Para una distribución de probabilidad f en U, calcularemos la probabilidad como:
y el grado de verdad E(p) de la proposición p, con el calificador P, se calculará aplicando la función que representa P sobre la probabilidad de la proposición sin calificador:
Los posibles valores de P se representan con etiquetas de la forma: "probable", "muy probable", "improbable", etc. cuyo significado viene dado por curvas como las representadas en la figura A-3
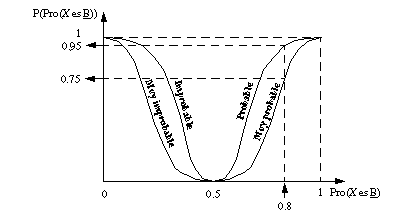
Por ejemplo, supongamos una variable T que representa la temperatura media diaria en ºC de una ciudad concreta en un mes del año. Supongamos una proposición de la forma "la temperatura T está alrededor de 20 ºC", y que conocemos la definición del conjunto borroso "alrededor de 20 ºC" y la función f de densidad de probabilidad para los diferentes valores de T; entonces podemos calcular la probabilidad de esta proposición aplicando la fórmula [EC. A.38] ; supongamos que es 0.8. Aplicando diferentes calificadores de probabilidad se obtienen proposiciones con diferentes valores de verdad; por ejemplo, para p = "es probable que la temperatura T esté alrededor de 20 ºC" el grado de verdad será 0.95 (ver figura A-3 ), pero para la proposición "es muy probable que la temperatura T esté alrededor de 20 ºC" será sólo 0.75.
Una proposición p de este tipo se expresa por la forma canónica:
p: Si X es A, entonces Y es B[EC. A.40]
donde X y Y son variables definidas en conjuntos universales UX y UY respectivamente, y A y B son conjuntos borrosos en UX y UY respectivamente. También se suelen representar con el símbolo "Æ" del condicional: A Æ B.
Estas proposiciones también pueden verse como proposiciones de la forma:
donde R es una relación borrosa (subconjunto borroso de UX ¥ UY), definida como ( [Fernández y Sáez-Vacas, 95] ) 5 :
Las proposiciones de este tipo se caracterizan por las siguientes formas canónicas:
p: Si X es A, entonces Y es B es V[EC. A.43]
donde V es un calificador del grado de verdad, o bien:
p: Pro(X es A | Y es B) es P[EC. A.44]
siendo P un calificador de la probabilidad condicionada Pro(X es A | Y es B).
Las etiquetas lingüísticas son adverbios de cantidad, como "muy", "bastante", "más o menos", etc., que se usan dentro de sentencias borrosas como modificadores de predicados borrosos, valores de verdad borrosos o probabilidades borrosas. Por ejemplo, la proposición "x es joven", cuyo significado se interpreta como "x es joven es verdadero", se puede modificar con la etiqueta "muy" de tres formas diferentes:
"x es muy joven es muy verdadero"
De forma similar, la sentencia "x es joven es probable" puede modificarse como "x es joven es muy probable", etc.
En general, una proposición borrosa de la forma p: x es B, y una etiqueta lingüística H, se puede construir una proposición modificada,
donde HB representa el predicado borroso obtenido al aplicar la etiqueta H al predicado original B. Otras modificaciones posibles resultan al aplicar H sobre el grado de verdad (equivalente a modificar el predicado borroso, apartado A.4.2.1 ) o el valor de probabilidad utilizados en la proposición dada ( apartado A.4.2.2 ).
Las etiquetas lingüísticas sólo se aplican en lógica borrosa, ya que en la clásica lógica booleana no tienen interpretación posible sentencias como "muy horizontal", "muy rectángulo", etc.
Cualquier etiqueta lingüística H puede interpretarse como una función h, que se denomina modificador, definida en el intervalo unidad [0, 1]:
Dado un predicado borroso B, el significado del predicado HB modificado se obtendrá aplicando la función h, asociada a la etiqueta H, sobre el grado de verdad del predicado sin modificador:
Se denominan modificadores fuertes a aquéllos en los que h(a) < a, para todo a perteneciente al intervalo [0, 1], mientras que los débiles son aquéllos en los que h(a) > a. El modificador identidad es aquél en el que h(a) = a. Cualquier modificador debe cumplir las siguientes propiedades ( [Klir y Yuan, 95] ):
Generalmente se utiliza la siguiente clase de funciones
ha(a) = aa, a [0, 1], a ¬+[EC. A.48]
para definir los modificadores asociados a las etiquetas lingüísticas. Cuando a < 1, ha es un modificador débil; cuando a > 1, ha es fuerte; y h1 es el modificador identidad. Algunas definiciones de modificadores podrían ser ( [Zadeh, 73] ):
1. Una frecuente mala interpretación de la lógica borrosa se debe a que ésta puede considerarse, en un sentido muy restringido, como una extensión y generalización de las clásicas lógicas multivaloradas para infinitos valores de verdad. Sin embargo, la lógica borrosa va más allá, porque no sólo considera que hay una infinidad de valores semánticos entre "verdadero" y "falso", sino que también tiene en cuenta que esos mismos valores de verdad son imprecisos ( [Fernández y Sáez-Vacas, 87] ).
2. La unión e intersección de conjuntos borrosos se definen, en general, como funciones de la forma:
t.q. mf [A,B](x) = f [mA(x) , mB(x)]
que debe cumplir ciertos axiomas (véase [Klir y Folger, 88] ). Existen diferentes clases de funciones cuyos elementos satisfacen todos los requerimientos impuestos a estas funciones borrosas (funciones de: Yager, Schweizer & Sklar, Hamacher, Frank, Dombi, etc.).
Por ejemplo, la clase de funciones de Yager para la unión de conjuntos borrosos viene definida por la expresión:
uw(a, b) = min [1, (aw+bw)1/w], donde w (0, ·)
Dentro de esta clase, tiene especial interés la función obtenida para el valor w = ·, pues es la clásica definición de la unión borrosa:
u·(a, b) = lim(wÆ·) { min[1, (aw+bw)1/w] } = max(a, b)
De modo análogo, de la clase de funciones de intersección de Yager, para el valor w = ·, se obtiene la clásica definición de la intersección borrosa:
i·(a, b) = lim(wÆ·) { min[1, ((1-a)w + (1-b)w)1/w] } = min(a, b)
3. Como ya se ha mencionado, los grados de pertenencia a un conjunto borroso no son (necesariamente) probabilidades. Sin embargo, cualquier distribución de probabilidad puede interpretarse como un conjunto borroso.
4. Como se comenta en el apartado A.1.1 , hay que destacar dos posibles notaciones para el grado de pertenencia a una relación borrosa (conjunto borroso en general): en una de ellas se utiliza el mismo símbolo P con que se representa a la relación borrosa; en la otra, por el contrario, se utiliza el símbolo mP para el grado de pertenencia a la relación P. Aquí seguiremos esta segunda notación, que, por otro lado, es la más tradicional.
5. Son posibles otras definiciones, por ejemplo, aplicando las leyes de Lukasiewicz ( [Klir y Yuan, 95] ):